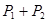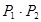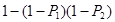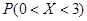题目内容
某课程考核分理论与实验两部分进行,每部分考核成绩只记“合格”与“不合格”,两部分考核都是“合格”,则该课程考核“合格”,若甲、乙、丙三人在理论考核中合格的概率分别为0.9,0.8,0.7,在实验考核中合格的概率分别为0.8,0.7,0.9,所有考核是否合格相互之间没有影响.
(1)求甲、乙、丙三人在理论考核中至少有两人合格的概率;
(2)求这三个人该课程考核都合格的概率(结果保留三位小数).
(1)求甲、乙、丙三人在理论考核中至少有两人合格的概率;
(2)求这三个人该课程考核都合格的概率(结果保留三位小数).
(1) 0.902 (2) 0.254
解:记“甲理论考核合格”为事件A1,“乙理论考核合格”为事件A2,“丙理论考核合格”为事件A3,记事件
 i为Ai的对立事件,i=1,2,3.记“甲实验考核合格”为事件B1,“乙实验考核合格”为事件B2,“丙实验考核合格”为事件B3.
i为Ai的对立事件,i=1,2,3.记“甲实验考核合格”为事件B1,“乙实验考核合格”为事件B2,“丙实验考核合格”为事件B3.(1)记“理论考核中至少有两人合格”为事件C,记
 为事件C的对立事件,
为事件C的对立事件,P(C)=P(A1A2A3+A1A2
 +A1
+A1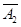 A3+
A3+ A2A3)
A2A3)=P(A1A2A3)+P(A1A2
 )+P(A1
)+P(A1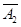 A3)+P(
A3)+P( A2A3)
A2A3)=0.9×0.8×0.7+0.9×0.8×0.3+0.9×0.2×0.7+0.1×0.8×0.7=0.902.
所以,理论考核中至少有两人合格的概率为0.902.
(2)记“三个人该课程考核都合格”为事件D.
P(D)=P[(A1·B1)·(A2·B2)·(A3·B3)]
=P(A1·B1)·P(A2·B2)·P(A3·B3)
=P(A1)·P(B1)·P(A2)·P(B2)·P(A3)·P(B3)
=0.9×0.8×0.8×0.7×0.7×0.9≈0.254.
所以,这三个人该课程考核都合格的概率为0.254.

练习册系列答案
相关题目
 元,求
元,求 ,
, ,
, ,则此密码能被译出的概率为________.
,则此密码能被译出的概率为________.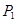 ,乙射中目标的概率为
,乙射中目标的概率为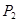 ,两人各射击1次,那么甲、乙至少有一个射中目标的概率为( )
,两人各射击1次,那么甲、乙至少有一个射中目标的概率为( )