题目内容
将含有3n个正整数的集合M分成元素个数相等且两两没有公共元素的三个集合A、B、C,其
中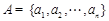 ,
,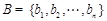 ,
,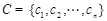 ,若A、B、C中的元素满足条件:
,若A、B、C中的元素满足条件: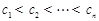 ,
,
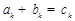 ,
,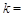 1,2,…,
1,2,…,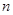 ,则称
,则称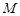 为“完并集合”.
为“完并集合”.
(1)若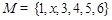 为“完并集合”,则
为“完并集合”,则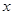 的一个可能值为
.(写出一个即可)
的一个可能值为
.(写出一个即可)
(2)对于“完并集合”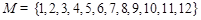 ,在所有符合条件的集合
,在所有符合条件的集合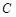 中,其元素乘积最小的集合是
.
中,其元素乘积最小的集合是
.
【答案】
(1)7、9、11中任一个;(2)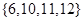 .
.
【解析】
试题分析:(1)由题意,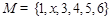 分成元素个数相等且两两没有公共元素的三个集合A、B、C,
分成元素个数相等且两两没有公共元素的三个集合A、B、C,
设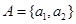 、
、 、
、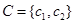 ,其中
,其中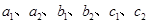 是
是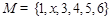 中的元素,
中的元素,
且互不相等.由定义可知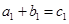 、
、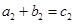 ,
,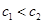 ,又它们都是正整数,所以
,又它们都是正整数,所以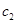 是
是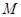 中最大的元
中最大的元
素.又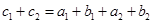 ,所以
,所以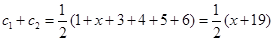 ,又
,又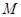 中元素为正整数,
中元素为正整数,
故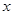 为正奇数.又由集合元素的互异性,
为正奇数.又由集合元素的互异性,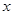 最小可为7,由
最小可为7,由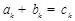 ,因为5+6=11可知
,因为5+6=11可知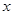 最大可为11,
最大可为11,
否则就不存在两个数的和等于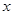 了.所以
了.所以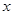 的一个可能值为7、9、11中任一个;(2)因为
的一个可能值为7、9、11中任一个;(2)因为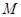 有12个元素,
有12个元素,
所以集合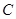 有4个元素,设
有4个元素,设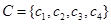 ,易知
,易知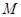 中元素之和为78,所以
中元素之和为78,所以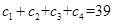 ,其中
,其中
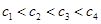 ,
,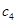 为
为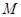 中最大元素,所以
中最大元素,所以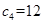 ,
, 最大可分别取10、11,所以
最大可分别取10、11,所以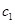 最小可等于
最小可等于
39-12-11-10=6,即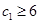 .所以集合
.所以集合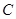 的所有可能的集合有:①
的所有可能的集合有:①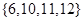 ②
②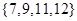 ③
③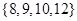
共三种,计算可知,元素乘积最小的集合为第①种——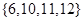 .
.
考点:新概念的理解、集合的含义

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
 ,
,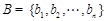 ,
,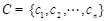 ,若A、B、C中的元素满足条件:
,若A、B、C中的元素满足条件: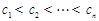 ,
,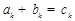 ,
,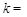 1,2,…,
1,2,…,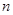 ,则称
,则称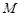 为“完并集合”.
为“完并集合”.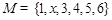 为“完并集合”,则
为“完并集合”,则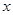 的一个可能值为 .(写出一个即可)
的一个可能值为 .(写出一个即可) 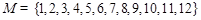 ,在所有符合条件的集合
,在所有符合条件的集合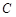 中,其元素乘积最小的集合是 .
中,其元素乘积最小的集合是 .