题目内容
若不等式5-x>7|x+1|与不等式ax2+bx-2>0同解,而|x-a|+|x-b|≤k的解集为空集,求实数k的取值范围.
【答案】分析:先将“不等式5-x>7|x+1|”转化为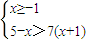 和
和 两种情况求解,最后取并集,再由“与不等式ax2+bx-2>0同解”,利用韦达定理求得a,b,最后由“|x-a|+|x-b|≤k的解集为空集”求得“|x-a|+|x-b|”最小值即可.
两种情况求解,最后取并集,再由“与不等式ax2+bx-2>0同解”,利用韦达定理求得a,b,最后由“|x-a|+|x-b|≤k的解集为空集”求得“|x-a|+|x-b|”最小值即可.
解答:解: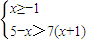 得
得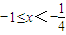
或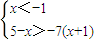 得-2<x<-1 (3分)
得-2<x<-1 (3分)
综上不等式的解集为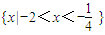 ,
,
又由已知与不等式ax2+bx-2>0同解,
所以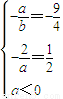 解得
解得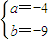 (7分)
(7分)
则|x-a|+|x-b|≥|x-a-x+b|=|b-a|=5,
所以当|x-a|+|x-b|≤k的解为空集时,k<5. (10分)
点评:本题主要考查绝对值不等式的解法,一元二次不等式的解集与相应方程根的关系,以及不等式恒成立问题.
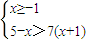 和
和 两种情况求解,最后取并集,再由“与不等式ax2+bx-2>0同解”,利用韦达定理求得a,b,最后由“|x-a|+|x-b|≤k的解集为空集”求得“|x-a|+|x-b|”最小值即可.
两种情况求解,最后取并集,再由“与不等式ax2+bx-2>0同解”,利用韦达定理求得a,b,最后由“|x-a|+|x-b|≤k的解集为空集”求得“|x-a|+|x-b|”最小值即可.解答:解:
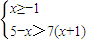 得
得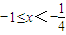
或
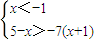 得-2<x<-1 (3分)
得-2<x<-1 (3分)综上不等式的解集为
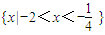 ,
,又由已知与不等式ax2+bx-2>0同解,
所以
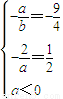 解得
解得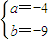 (7分)
(7分)则|x-a|+|x-b|≥|x-a-x+b|=|b-a|=5,
所以当|x-a|+|x-b|≤k的解为空集时,k<5. (10分)
点评:本题主要考查绝对值不等式的解法,一元二次不等式的解集与相应方程根的关系,以及不等式恒成立问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目