题目内容
四面体ABCD中，棱AB、AC、AD两两互相垂直，则顶点A在底面BCD上的正投影H为△BCD的（ ）
分析：连接BH、DH，可以先证明出AB与平面ACD垂直，然后得到CD与AB垂直，再结合CD与AH垂直得到CD垂直于平面ABH，从而BH垂直于CD，同样的我们可以证出DH垂直于BC，从而得出点H是三角形BDC的垂心．
解答：解：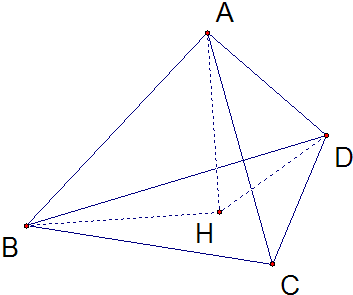
如图，连接BH、DH
∵BA⊥CA，BA⊥DA，CA∩DA=A
∴BA⊥平面ACD，结合CD?平面ACD
∴CD⊥BA
又∵AH⊥平面BDC，CD?平面BDC
∴CD⊥AH
∵AH∩BA=A
∴CD⊥平面ABH，得到BH⊥CD
所以BH为DC边上的高
同理可得DH为BC边上的高
因此H为三角形BDC的垂心．
故选A
如图，连接BH、DH∵BA⊥CA，BA⊥DA，CA∩DA=A
∴BA⊥平面ACD，结合CD?平面ACD
∴CD⊥BA
又∵AH⊥平面BDC，CD?平面BDC
∴CD⊥AH
∵AH∩BA=A
∴CD⊥平面ABH，得到BH⊥CD
所以BH为DC边上的高
同理可得DH为BC边上的高
因此H为三角形BDC的垂心．
故选A
点评：本题考查了三垂线定理及其逆定理在多面体中的应用，属于中档题．利用直线与平面垂直的判定与性质，反复运用线线垂直到线面垂直的相互转化，是解答本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
与
的夹角为_______;(
+
)·
=________.
与
的夹角；
·（
）.
与
的夹角；
·（
）.