题目内容
在等差数列{an}中,a1=142,d=-2,从第一项起,每隔两项取出一项,构成新的数列{bn},则此数列的前n项和Sn取得最大值时n的值是( ).
| A.23 | B.24 | C.25 | D.26 |
B
解析

练习册系列答案
相关题目
在等差数列 中,已知
中,已知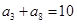 ,则
,则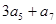 =( )
=( )
| A.10 | B.18 | C.20 | D.28 |
在等差数列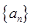 中,
中,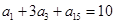 ,则
,则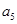 的值为( )
的值为( )
| A.2 | B.3 | C.4 | D.5 |
在等差数列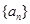 中,已知
中,已知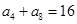 ,则该数列前11项的和
,则该数列前11项的和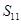 等于
等于
| A.58 | B.88 | C.143 | D.176 |
已知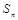 为等差数列
为等差数列 的前
的前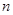 项和,
项和,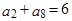 ,则
,则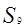 为( )
为( )
A.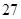 | B.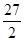 | C.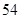 | D.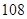 |
设等差数列{an}的前n项和为Sn,Sm-1=-2,Sm=0,
Sm+1=3,则m等于( ).
| A.3 | B.4 | C.5 | D.6 |
已知等差数列{an}的前n项和为Sn,且S3=6,则5a1+a7的值为( )
| A.12 | B.10 | C.24 | D.6 |
设{an}是公差不为0的等差数列,a1=2且a1,a3,a6成等比数列,则{an} 的前n项和Sn=( ).
A.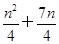 | B.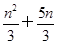 | C.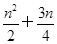 | D.n2+n |
在数列{an}中,a1=1,a2=2,且an+2-an=1+(-1)n(n∈N*),则S10=( ).
| A.2100 | B.2600 | C.2800 | D.3100 |