题目内容
已知函数y=ax与y=-| b | x |
分析:利用正比例函数与反比例函数的单调性得到a,b的范围;求出三次函数的导函数,令导函数小于0 求出x的范围即为函数的得到递减区间.
解答:解:根据题意a<0,b<0.
由y=ax3+bx2+5,得y′=3ax2+2bx,
令y′<0,可得x>0或x<-
,
故所求减区间为(-∞,-
)和(0,+∞).
故答案为:(-∞,-
)和(0,+∞)
由y=ax3+bx2+5,得y′=3ax2+2bx,
令y′<0,可得x>0或x<-
| 2b |
| 3a |
故所求减区间为(-∞,-
| 2b |
| 3a |
故答案为:(-∞,-
| 2b |
| 3a |
点评:本题考查函数的单调性与导函数符号的关系:f′(x)>0则f(x)单增;当f′(x)<0则f(x)递减.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目

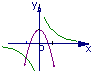


 在(0,+∞)上都是减函数,则函数y=ax3+bx2+5的单调减区间为 .
在(0,+∞)上都是减函数,则函数y=ax3+bx2+5的单调减区间为 .