题目内容
我们把平面内两条相交但不垂直的数轴构成的坐标系(两条数轴的原点重合且单位长度相同)称为斜坐标系.平面上任意一点P的斜坐标定义为:若| OP |
| e1 |
| e2 |
| e1 |
| e2 |
分析:先建立斜坐标系,找出对应关系,最后由余弦定理可得答案.
解答: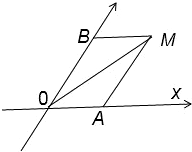 解:依题意建立斜坐标系:
解:依题意建立斜坐标系:
则A(1,0),B(0,2),M(1,2),∠AOB=60°,∠OAM=120°
四边形OAMB为平行四边形,∴|OA|=1|AM|=|OB|=2,
由余弦定理可得:|OM|2=|OA|2+|AM|2-2|OA||AM|cos120°=7
∴|OM|=
,
故答案为:
.
 解:依题意建立斜坐标系:
解:依题意建立斜坐标系:则A(1,0),B(0,2),M(1,2),∠AOB=60°,∠OAM=120°
四边形OAMB为平行四边形,∴|OA|=1|AM|=|OB|=2,
由余弦定理可得:|OM|2=|OA|2+|AM|2-2|OA||AM|cos120°=7
∴|OM|=
| 7 |
故答案为:
| 7 |
点评:本题主要考查余弦定理的运用.基础题.

练习册系列答案
相关题目
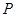 的斜坐标定义为:若
的斜坐标定义为:若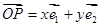 (其中
(其中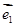 、
、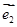 分别为斜坐标系的
分别为斜坐标系的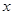 轴、
轴、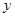 轴正方向上的单位向量,
轴正方向上的单位向量,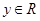 ),则点
),则点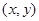 .在平面斜坐标系
.在平面斜坐标系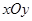 中,若
中,若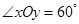 ,已知点
,已知点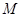 的斜坐标为
的斜坐标为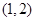 ,则点
,则点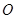 的距离为 .
的距离为 . 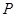 的斜坐标定义为:若
的斜坐标定义为:若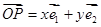 (其中
(其中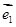 、
、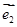 分别为斜坐标系的
分别为斜坐标系的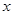 轴、
轴、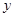 轴正方向上的单位向量,
轴正方向上的单位向量,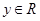 ),则点
),则点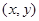 .在平面斜坐标系
.在平面斜坐标系 中,若
中,若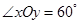 ,已知点
,已知点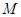 的斜坐标为
的斜坐标为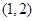 ,则点
,则点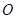 的距离为
. [来源:]
的距离为
. [来源:]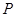 的斜坐标定义为:若
的斜坐标定义为:若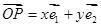 (其中
(其中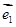 、
、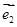 分别为斜坐标系的
分别为斜坐标系的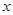 轴、
轴、 轴正方向上的单位向量,
轴正方向上的单位向量,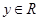 ),则点
),则点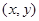 .在平面斜坐标系
.在平面斜坐标系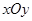 中,若
中,若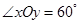 ,已知点
,已知点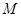 的斜坐标为
的斜坐标为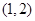 ,则点
,则点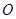 的距离为
.
的距离为
. 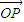 =x
=x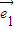 +y
+y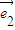 (其中
(其中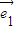 、
、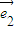 分别为斜坐标系的x轴、y轴正方向上的单位向量,x、y∈R),则点P的斜坐标为(x,y).在平面斜坐标系xoy中,若∠xoy=60°,已知点M的斜坐标为(1,2),则点M到原点O的距离为 .
分别为斜坐标系的x轴、y轴正方向上的单位向量,x、y∈R),则点P的斜坐标为(x,y).在平面斜坐标系xoy中,若∠xoy=60°,已知点M的斜坐标为(1,2),则点M到原点O的距离为 .