题目内容
已知函数 y = f (x) 是定义在R上的增函数,函数 y = f (x-1) 的图象关于点 (1, 0)对称. 若对任意的 x, y∈R,不等式 f (x2-6x + 21) + f (y2-8y) < 0 恒成立,则当 x > 3 时,x2 + y2 的取值范围是( )
A.(3, 7) B.(9, 25) C.(13, 49) D. (9, 49)
【答案】
C
【解析】解:∵函数y=f(x-1)的图象关于点(1,0)对称,
∴函数y=f(x)的图象关于点(0,0)对称,
即函数y=f(x)为奇函数,则f(-x)=-f(x),
又∵f(x)是定义在R上的增函数且f(x2-6x+21)+f(y2-8y)<0恒成立
∴(x2-6x+21)<-f(y2-8y)=f(8y-y2)恒成立,
∴x2-6x+21<8y-y2,
∴(x-3)2+(y-4)2<4恒成立,
设M (x,y),则当x>3时,M表示以(3,4)为圆心2为半径的右半圆内的任意一点,
则d=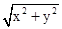 表示区域内的点和原点的距离.
表示区域内的点和原点的距离.
由下图可知:d的最小值是OA=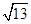
OB=OC+CB,5+2=7,
当x>3时,x2+y2的范围为(13,49)
故答案为:(13,49)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 sinx在[0,π]上的大致图象是( )
sinx在[0,π]上的大致图象是( )


