题目内容
已知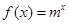 (m为常数,m>0且m≠1).
(m为常数,m>0且m≠1).
设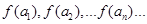 (n∈
(n∈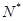 ?)是首项为m2,公比为m的等比数列.
?)是首项为m2,公比为m的等比数列.
(1)求证:数列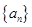 是等差数列;
是等差数列;
(2)若 ,且数列
,且数列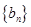 的前n项和为Sn,当m=2时,求Sn;
的前n项和为Sn,当m=2时,求Sn;
【答案】
(1)见解析(2)2n+2·n
【解析】本题考查数列的定义的应用,错位相减法,数列与函数相结合,恒成立问题的综合应用,考查分析问题解决问题,转化思想的应用,知识面广,运算量大.
(1)利用f (x)=mx(m为常数,m>0且m≠1).代入an,求出an的表达式,利用等差数列的定义,证明数列{an}是等差数列;
(2)通过bn=an f (an),且数列{bn}的前n项和为Sn,当m=2时,求出Sn的表达式,利用错位相减法求出Sn;
解:(1)由题意f(an)=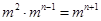 ,即
,即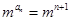 .
.
∴an=n+1,(2分) ∴an+1-an=1,
∴数列{an}是以2为首项,1为公差的等差数列.
(2)由题意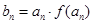 =(n+1)·mn+1,
=(n+1)·mn+1,
当m=2时,bn=(n+1)·2n+1
∴Sn=2·22+3·23+4·24+…+(n+1)·2n+1 ①
①式两端同乘以2,得
2Sn=2·23+3·24+4·25+…+n·2n+1+(n+1)·2n+2 ②
②-①并整理,得
Sn=-2·22-23-24-25-…-2n+1+(n+1)·2n+2
=-22-(22+23+24+…+2n+1)+(n+1)·2n+2
=-22-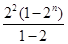 +(n+1)·2n+2
+(n+1)·2n+2
=-22+22(1-2n)+(n+1)·2n+2=2n+2·n.

练习册系列答案
相关题目
 (m为常数,m>0且
(m为常数,m>0且 ),设
),设 是首项为4,公差为2的等差数列.
是首项为4,公差为2的等差数列.  ,且数列{bn}的前n项和Sn,当
,且数列{bn}的前n项和Sn,当 时,求
时,求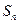 ;
; ,问是否存在m,使得{cn}中每一项恒小于它后面的项?若存在,
,问是否存在m,使得{cn}中每一项恒小于它后面的项?若存在,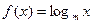 (m为常数,m>0且
(m为常数,m>0且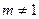 )
)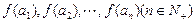 是首项为4,公差为2的等差数列.
是首项为4,公差为2的等差数列. 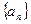 是等比数列;
是等比数列;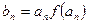 ,且数列{bn}的前n项和
,且数列{bn}的前n项和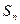 ,当
,当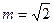 时,求
时,求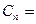
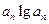 ,问是否存在
,问是否存在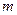 ,使得
,使得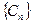 中每一项恒小于它后面的项?
中每一项恒小于它后面的项?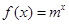 (m为常数,m>0且m≠1).
(m为常数,m>0且m≠1).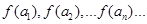 (n∈
(n∈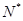 ?)是首项为m2,公比为m的等比数列.
?)是首项为m2,公比为m的等比数列.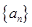 是等差数列;
是等差数列; 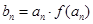 ,且数列
,且数列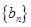 的前n项和为Sn,当m=2时,求Sn;
的前n项和为Sn,当m=2时,求Sn;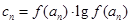 ,问是否存在m,使得数列
,问是否存在m,使得数列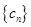 中每一项恒小于它后面的项?若存在,求出m的范围;若不存在,请说明理由.
中每一项恒小于它后面的项?若存在,求出m的范围;若不存在,请说明理由.