题目内容
已知两定点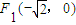 ,
,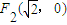 ,满足条件
,满足条件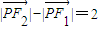 的点P的轨迹是曲线E,直线y=kx-1与曲线E交于A、B两点.
的点P的轨迹是曲线E,直线y=kx-1与曲线E交于A、B两点.(Ⅰ)求k的取值范围;
(Ⅱ)如果
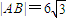 且曲线E上存在点C,使
且曲线E上存在点C,使 求m的值和△ABC的面积S.
求m的值和△ABC的面积S.
【答案】分析:(Ⅰ)首先根据曲线的定义判断出曲线E是双曲线的左支,a和c已知,则可求得b,曲线E的方程可得.设出A,B的坐标,把直线方程与双曲线方程联立消去y,进而根据直线与双曲线左支交于两点A,B,联立不等式求得k的范围.
(Ⅱ)根据弦长公式求得|AB|的表达式,根据结果为6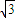 求得k,则直线AB的方程可得,设C(x,y),根据
求得k,则直线AB的方程可得,设C(x,y),根据 ,可得
,可得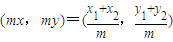 ;根据x1+x2和y1+y2的值求得C点的坐标,代入双曲线方程求得m的值,进而求得点C到直线AB的距离,最后利用三角形面积公式求得三角形ABC的面积.
;根据x1+x2和y1+y2的值求得C点的坐标,代入双曲线方程求得m的值,进而求得点C到直线AB的距离,最后利用三角形面积公式求得三角形ABC的面积.
解答: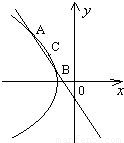 解:(Ⅰ)由双曲线的定义可知,曲线E是以
解:(Ⅰ)由双曲线的定义可知,曲线E是以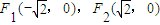 为焦点的双曲线的左支,
为焦点的双曲线的左支,
且 ,易知b=1
,易知b=1
故曲线E的方程为x2-y2=1(x<0)
设A(x1,y1),B(x2,y2),由题意建立方程组
消去y,得(1-k2)x2+2kx-2=0
又已知直线与双曲线左支交于两点A,B,有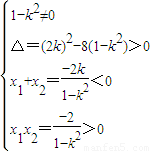
解得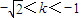 .
.
(Ⅱ)∵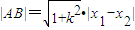
=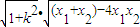 =
=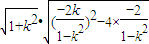
=
依题意得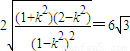
整理后得28k4-55k2+25=0
∴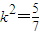 或
或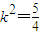
但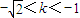 ∴
∴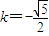
故直线AB的方程为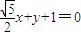
设C(x,y),由已知 ,得(x1,y1)+(x2,y2)=(mx,my)
,得(x1,y1)+(x2,y2)=(mx,my)
∴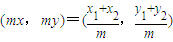 ,(m≠0)
,(m≠0)
又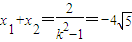 ,
,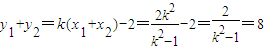
∴点C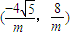
将点C的坐标代入曲线E的方程,得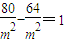 得m=±4,
得m=±4,
但当m=-4时,所得的点在双曲线的右支上,不合题意
∴m=4,点C的坐标为 C到AB的距离为
C到AB的距离为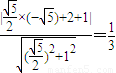
∴△ABC的面积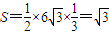
点评:本小题主要考查双曲线的定义和性质、直线与双曲线的关系、点到直线的距离等知识及解析几何的基本思想、方法和综合解决问题的能力.
(Ⅱ)根据弦长公式求得|AB|的表达式,根据结果为6
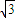 求得k,则直线AB的方程可得,设C(x,y),根据
求得k,则直线AB的方程可得,设C(x,y),根据 ,可得
,可得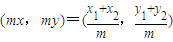 ;根据x1+x2和y1+y2的值求得C点的坐标,代入双曲线方程求得m的值,进而求得点C到直线AB的距离,最后利用三角形面积公式求得三角形ABC的面积.
;根据x1+x2和y1+y2的值求得C点的坐标,代入双曲线方程求得m的值,进而求得点C到直线AB的距离,最后利用三角形面积公式求得三角形ABC的面积.解答:
 解:(Ⅰ)由双曲线的定义可知,曲线E是以
解:(Ⅰ)由双曲线的定义可知,曲线E是以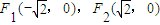 为焦点的双曲线的左支,
为焦点的双曲线的左支,且
 ,易知b=1
,易知b=1故曲线E的方程为x2-y2=1(x<0)
设A(x1,y1),B(x2,y2),由题意建立方程组

消去y,得(1-k2)x2+2kx-2=0
又已知直线与双曲线左支交于两点A,B,有
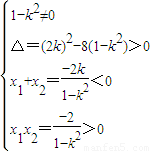
解得
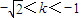 .
.(Ⅱ)∵
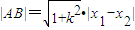
=
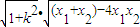 =
=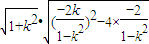
=

依题意得
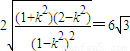
整理后得28k4-55k2+25=0
∴
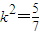 或
或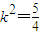
但
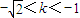 ∴
∴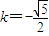
故直线AB的方程为
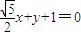
设C(x,y),由已知
 ,得(x1,y1)+(x2,y2)=(mx,my)
,得(x1,y1)+(x2,y2)=(mx,my)∴
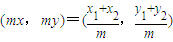 ,(m≠0)
,(m≠0)又
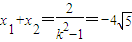 ,
,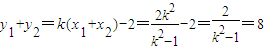
∴点C
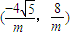
将点C的坐标代入曲线E的方程,得
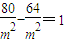 得m=±4,
得m=±4,但当m=-4时,所得的点在双曲线的右支上,不合题意
∴m=4,点C的坐标为
 C到AB的距离为
C到AB的距离为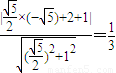
∴△ABC的面积
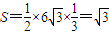
点评:本小题主要考查双曲线的定义和性质、直线与双曲线的关系、点到直线的距离等知识及解析几何的基本思想、方法和综合解决问题的能力.

练习册系列答案
相关题目
 ,动点P满足
,动点P满足 ,由点P向x轴作垂线PQ,垂足为Q,点M满足
,由点P向x轴作垂线PQ,垂足为Q,点M满足 ,点M的轨迹为C.
,点M的轨迹为C.