题目内容
设首项为正数的等比数列,它的前n项和为80,且其中数值最大的项是54,前2n项和为6 560,求此数列的通项.
解:设此等比数列的首项为a1,公比q≠1,
则有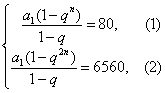
两式相除得qn=81.
将其反代回(1)中,得a1=q-1. (3)
∵a1>0,∴q>1.
故已知数列是递增数列.则54是数列中第n项的值,即an=54![]() a1qn-1=54.∴a1qn=54q,即81a1=54q.
a1qn-1=54.∴a1qn=54q,即81a1=54q.
代入(3)得q=3,a1=2.∴an=2·3n-1.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 =1024.对满足at>128的任意正整数t,函数f(t)=
=1024.对满足at>128的任意正整数t,函数f(t)=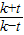 的最小值是 .
的最小值是 .