题目内容
已知圆C：（x+cosθ）2+（y-sinθ）2=1，那么直线l：ax+by=0与圆的位置关系是
- A.相离或相切
- B.相交或相切
- C.一定相交
- D.不能确定
B
分析：确定圆的圆心与半径，求出圆心到直线的距离，与半径比较，即可得到结论．
解答：圆C：（x+cosθ）2+（y-sinθ）2=1的圆心坐标为（-cosθ，sinθ），圆的半径为1
则圆心到直线的距离为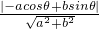
=
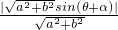≤1
∴直线l：ax+by=0与圆的位置关系是相交或相切
故选B．
点评：本题考查直线与圆的位置关系，考查点到直线的距离公式，属于中档题．
分析：确定圆的圆心与半径，求出圆心到直线的距离，与半径比较，即可得到结论．
解答：圆C：（x+cosθ）2+（y-sinθ）2=1的圆心坐标为（-cosθ，sinθ），圆的半径为1
则圆心到直线的距离为
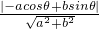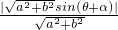=≤1∴直线l：ax+by=0与圆的位置关系是相交或相切
故选B．
点评：本题考查直线与圆的位置关系，考查点到直线的距离公式，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
（本题满分15分）17. (本小题满分15分)已知圆C：
，圆C关于直线
对称，圆心在第二象限，半径为
。W ww.k s5 u.co m
与圆C相切，且在x轴、y轴上的截距相等，求直线
（本题满分15分）17. (本小题满分15分)已知圆C：
，圆C关于直线
对称，圆心在第二象限，半径为
。W ww.k s5 u.co m
与圆C相切，且在x轴、y轴上的截距相等，求直线
，且过点P（1，1）．