题目内容
本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
已知椭圆 :
: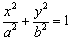 (
( ),其焦距为
),其焦距为 ,若
,若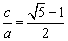 (
(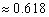 ),则称椭圆
),则称椭圆 为“黄金椭圆”.
为“黄金椭圆”.
(1)求证:在黄金椭圆 :
: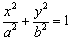 (
( )中,
)中,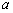 、
、 、
、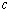 成等比数列.
成等比数列.
(2)黄金椭圆 :
: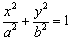 (
( )的右焦点为
)的右焦点为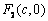 ,
, 为椭圆
为椭圆 上的
上的
任意一点.是否存在过点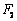 、
、 的直线
的直线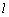 ,使
,使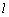 与
与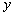 轴的交点
轴的交点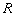 满足
满足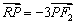 ?若存在,求直线
?若存在,求直线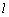 的斜率
的斜率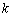 ;若不存在,请说明理由.
;若不存在,请说明理由.
(3)在黄金椭圆中有真命题:已知黄金椭圆 :
: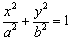 (
( )的左、右
)的左、右
焦点分别是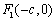 、
、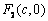 ,以
,以 、
、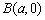 、
、 、
、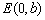 为顶点的菱形
为顶点的菱形 的内切圆过焦点
的内切圆过焦点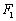 、
、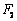 .
.
试写出“黄金双曲线”的定义;对于上述命题,在黄金双曲线中写出相关的真命题,并加以证明.
【答案】
(1)证明:由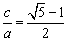 及
及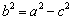 ,得
,得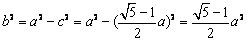
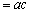 ,故
,故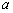 、
、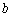 、
、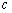 成等比数列.
成等比数列.
(2)解:由题设,显然直线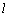 垂直于
垂直于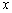 轴时不合题意,设直线
轴时不合题意,设直线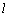 的方程为
的方程为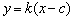 ,
,
得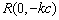 ,又
,又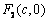 ,及
,及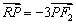
 ,得点
,得点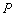 的坐标为
的坐标为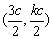 ,(6分)
,(6分)
因为点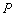 在椭圆上,所以
在椭圆上,所以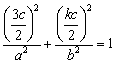 ,又
,又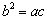 ,得
,得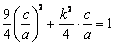 ,
,
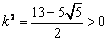 ,故存在满足题意的直线
,故存在满足题意的直线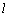 ,其斜率
,其斜率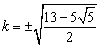 .
.
(3)黄金双曲线的定义:已知双曲线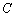 :
: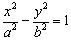 ,其焦距为
,其焦距为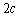 ,若
,若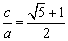 (或写成
(或写成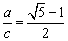
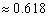 ),则称双曲线
),则称双曲线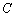 为“黄金双曲线”.
为“黄金双曲线”.
在黄金双曲线中有真命题:已知黄金双曲线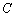 :
: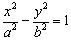 的左、右焦点分别是
的左、右焦点分别是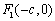 、
、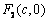 ,以
,以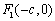 、
、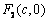 、
、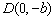 、
、 为顶点的菱形
为顶点的菱形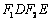 的内切圆过顶点
的内切圆过顶点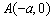 、
、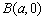 .
.
证明:直线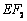 的方程为
的方程为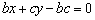 ,原点到该直线的距离为
,原点到该直线的距离为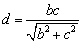 ,
,
将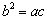 代入,得
代入,得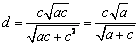 ,又将
,又将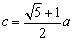 代入,化简得
代入,化简得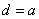 ,
,
故直线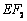 与圆
与圆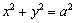 相切,同理可证直线
相切,同理可证直线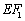 、
、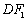 、
、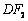 均与圆
均与圆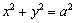 相切,即以
相切,即以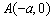 、
、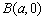 为直径的圆
为直径的圆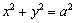 为菱形
为菱形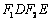 的内切圆,命题得证.
的内切圆,命题得证.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
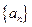 :
: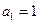 ,
, ,
, ,
, (
(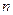 是正整数),与数列
是正整数),与数列 :
: ,
, ,
, ,
, ,
,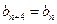 (
( .
. ,求
,求 的值;
的值; ;
; ,且存在正整数
,且存在正整数 ,使得在
,使得在 ,
, ,
, ,
, 中有4项为100.
中有4项为100. ,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为
,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为 ,公差为
,公差为 的无穷等差数列
的无穷等差数列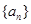 的子数列问题,为此,他取了其中第一项
的子数列问题,为此,他取了其中第一项 ,第三项
,第三项 和第五项
和第五项 .
. 成等比数列,求
成等比数列,求 ,
,  的无穷等差数列
的无穷等差数列 ,使得数列
,使得数列 ,公比为正整数
,公比为正整数 (
( )的无穷等比数 列
)的无穷等比数 列 ,总可以找到一个子数列
,总可以找到一个子数列 ,使得
,使得 ,由
,由 与
与 的大小关系去判断该命题是否正确. 他将得到什么结论?
的大小关系去判断该命题是否正确. 他将得到什么结论? ,对任意实数
,对任意实数 ,有
,有 恒成立;数列
恒成立;数列 满足
满足 .
. 的解析式和值域;
的解析式和值域; ,使得当
,使得当 时,数列
时,数列 ,是否存在非零整数
,是否存在非零整数 ,使得对任意
,使得对任意 ,都有
,都有
 恒成立,若存在,
恒成立,若存在,