题目内容
已知函数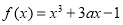 的导函数为
的导函数为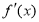 ,
,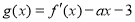 .
.
(1)当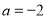 时,求函数
时,求函数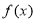 的单调区间;
的单调区间;
(2)若对满足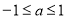 的一切
的一切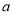 的值,都有
的值,都有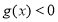 ,求实数
,求实数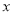 的取值范围;
的取值范围;
(3)若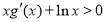 对一切
对一切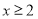 恒成立,求实数
恒成立,求实数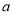 的取值范围.
的取值范围.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
已知函数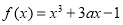 的导函数为
的导函数为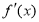 ,
,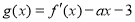 .
.
(1)当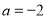 时,求函数
时,求函数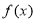 的单调区间;
的单调区间;
(2)若对满足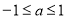 的一切
的一切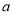 的值,都有
的值,都有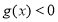 ,求实数
,求实数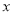 的取值范围;
的取值范围;
(3)若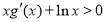 对一切
对一切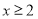 恒成立,求实数
恒成立,求实数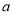 的取值范围.
的取值范围.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案