题目内容
证明:
,
,
不能为同一等差数列的三项.
| 2 |
| 3 |
| 5 |
分析:本题直接证明难度较大,可采用反证法,即假设
、
、
为同一等差数列的三项,进而根据等差数列的定义,分析出矛盾,进而得到原结论成立.
| 2 |
| 3 |
| 5 |
解答:证明:假设
、
、
为同一等差数列的三项,
则存在整数m,n满足
=
+md ①
=
+nd ②
①×n-②×m得:
n-
m=
(n-m)
两边平方得:3n2+5m2-2
mn=2(n-m)2
左边为无理数,右边为有理数,且有理数≠无理数
所以,假设不正确.
即
、
、
不能为同一等差数列的三项
| 2 |
| 3 |
| 5 |
则存在整数m,n满足
| 3 |
| 2 |
| 5 |
| 2 |
①×n-②×m得:
| 3 |
| 5 |
| 2 |
两边平方得:3n2+5m2-2
| 15 |
左边为无理数,右边为有理数,且有理数≠无理数
所以,假设不正确.
即
| 2 |
| 3 |
| 5 |
点评:本题考查的知识点是等差数列的定义,反证法,熟练掌握反证法的适用范围及证明步骤是解答的关键.

练习册系列答案
相关题目
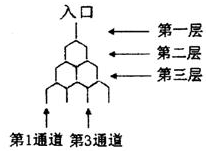 图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有一条的为第一层,有两条的为第二层,以此类推,竖直线段有n条的为第n层,每一层的竖直通道从左到右分别称为第1通道、第2通道,…,现在有一个小球从入口向下(只能向下,不能向上)运动,小球在每个交点处向左到达下一层或者向右到达下一层的可能性是相同的.小球到达第n层第m通道的不同路径数称为an,m,如小球到达第二层第1通道和第二层第2通道的路径都只有一种情况,因此,a2,1=1,a2,2=1.
图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有一条的为第一层,有两条的为第二层,以此类推,竖直线段有n条的为第n层,每一层的竖直通道从左到右分别称为第1通道、第2通道,…,现在有一个小球从入口向下(只能向下,不能向上)运动,小球在每个交点处向左到达下一层或者向右到达下一层的可能性是相同的.小球到达第n层第m通道的不同路径数称为an,m,如小球到达第二层第1通道和第二层第2通道的路径都只有一种情况,因此,a2,1=1,a2,2=1.