题目内容
(本题满分10分)已知圆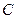 过点
过点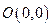 ,
,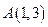 ,
,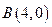 .
.
(1)求圆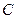 的方程;
的方程;
(2)设直线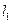 :
: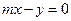 ,
,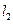 :
: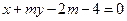 的交点为
的交点为 ,求证:点
,求证:点 必
必
圆 上.
上.
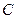 过点
过点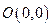 ,
,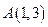 ,
,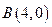 .
.(1)求圆
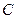 的方程;
的方程;(2)设直线
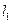 :
: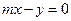 ,
,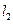 :
: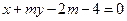 的交点为
的交点为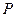 ,求证:点
,求证:点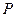 必
必圆
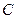 上.
上.
解:(1)设圆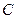 的方程为
的方程为 ,则
,则
 ……………………………………………………………2分
……………………………………………………………2分
解得
 圆
圆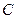 的方程为
的方程为 .…………………………………………5分
.…………………………………………5分
(2)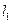 与
与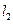 分别过定点(0,0)、(4,2),且两两垂直,………………………………7分
分别过定点(0,0)、(4,2),且两两垂直,………………………………7分
∴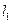 与
与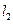 的交点
的交点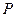 必在以(0,0)、(4,2)为一条直径的圆:………………8分
必在以(0,0)、(4,2)为一条直径的圆:………………8分
即在圆: 上,………………………………………………9分
上,………………………………………………9分
故:点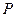 在圆
在圆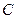
 上…………………………………………10分
上…………………………………………10分
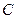 的方程为
的方程为 ,则
,则 ……………………………………………………………2分
……………………………………………………………2分解得

 圆
圆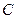 的方程为
的方程为 .…………………………………………5分
.…………………………………………5分(2)
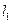 与
与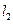 分别过定点(0,0)、(4,2),且两两垂直,………………………………7分
分别过定点(0,0)、(4,2),且两两垂直,………………………………7分∴
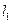 与
与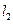 的交点
的交点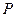 必在以(0,0)、(4,2)为一条直径的圆:………………8分
必在以(0,0)、(4,2)为一条直径的圆:………………8分即在圆:
 上,………………………………………………9分
上,………………………………………………9分故:点
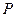 在圆
在圆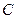
 上…………………………………………10分
上…………………………………………10分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 上移动。
上移动。 理由。
理由。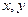 的方程
的方程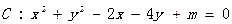 .
.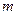 为何值时,方程
为何值时,方程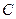 表示圆;
表示圆;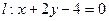 相交于M,N两点,且|MN|=
相交于M,N两点,且|MN|=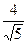 ,求
,求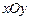 中,直线
中,直线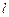 与
与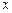 轴正半轴和
轴正半轴和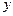 轴正半轴分别相交于
轴正半轴分别相交于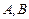 两点
两点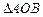 的内切圆为⊙
的内切圆为⊙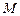
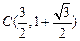 ,求直线
,求直线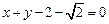 ,
,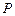 为⊙
为⊙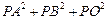 的最值
的最值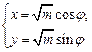 (φ为参数,m>0)相切,则m为 .
(φ为参数,m>0)相切,则m为 .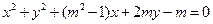 关于直线
关于直线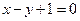 对称,则实数m的值为( )
对称,则实数m的值为( )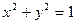 作两条切线PA、PB,则弦AB所在直线方程为( )
作两条切线PA、PB,则弦AB所在直线方程为( )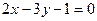 B.
B.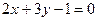
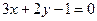 D.
D.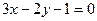
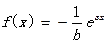 在
在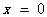 处的切线
处的切线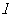 与圆
与圆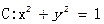 相离,则
相离,则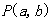 与圆
与圆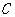 的位置关系是( )
的位置关系是( )