题目内容
（理科）若随机变量ξ～N（2，22），则
的值为 ．
【答案】分析：由题中条件：“随机变量ξ服从正态分布ξ～N（2，22）”，可得方差是4，则
的值为
．
解答：解；∵随机变量ξ服从正态分布ξ～N（2，22），
∴可得随机变量ξ方差是4，
∴
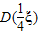的值为
（ξ）=
=
．
故答案为：
．
点评：本题主要考查正态分布的方差求法，离散型随机变量的期望与方差等，属于基础题．
的值为．解答：解；∵随机变量ξ服从正态分布ξ～N（2，22），
∴可得随机变量ξ方差是4，
∴
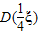的值为（ξ）==．故答案为：
．点评：本题主要考查正态分布的方差求法，离散型随机变量的期望与方差等，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
，乙投进的概率为
，两人投进与否要睛互没有影响．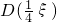
的值为________．