题目内容
将含有3n个正整数的集合M分成元素个数相等且两两没有公共元素的三个集合
A、B、C,其中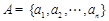 ,
,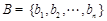 ,
,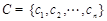 ,若A、B、C中的元素满足条件:
,若A、B、C中的元素满足条件: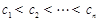 ,
,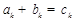 ,
,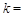 1,2,…,
1,2,…,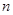 ,则称
,则称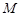 为“完并集合”.
为“完并集合”.
(1)若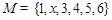 为“完并集合”,则
为“完并集合”,则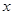 的一个可能值为 .(写出一个即可)
的一个可能值为 .(写出一个即可)
(2)对于“完并集合”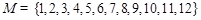 ,在所有符合条件的集合
,在所有符合条件的集合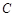 中,其元素乘积最小的集合是 .
中,其元素乘积最小的集合是 .
(1)7,9,11 中任一个 (2)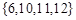
解析试题分析:(1)若集合A={1,4},B={3,5},根据完并集合的概念知集合C={6,x},∴x="4+3=7," 若集合A={1,5},B={3,6},根据完并集合的概念知集合C={4,x},∴x="5+6=11," 若集合A={1,3},B={4,6},根据完并集合的概念知集合C={5,x},∴x=3+6=9,故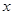 的一个可能值为7,9,11 中任一个;(2)若A={1,2,3,4},B={5,8,7,9},则C={6,10,12,11},若A={1,2,3,4},B="{5,6,8," 10 },则C={7,9,12,11},这两组比较得元素乘积最小的集合是
的一个可能值为7,9,11 中任一个;(2)若A={1,2,3,4},B={5,8,7,9},则C={6,10,12,11},若A={1,2,3,4},B="{5,6,8," 10 },则C={7,9,12,11},这两组比较得元素乘积最小的集合是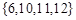
考点:本题考查了集合的新定义的运用
点评:这类题型的特点是在通过假设来给出一个新概念,在新情景下考查考生解决问题的迁移能力,要求解题者紧扣新概念,对题目中给出的条件抓住关键的信息,进行整理、加工、判断,实现信息的转化

练习册系列答案
相关题目
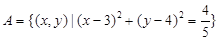 ,
,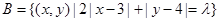 ,若
,若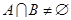 ,则实数
,则实数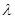 的取值范围是__________.
的取值范围是__________. ,则
,则 .
.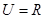 ,
,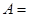
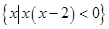 ,
,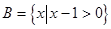 ,则
,则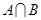 = .
= .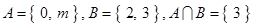 ,则实数
,则实数 .
. ,则
,则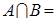 .
. ,
, ,且
,且 ,则实数
,则实数 的取值范围是
的取值范围是  ,若有
,若有 ,
, ,则
,则 的取值范围是 。
的取值范围是 。