题目内容
(一)已知a,b,c∈R+,
①求证:a2+b2+c2≥ab+bc+ac;
②若a+b+c=1,利用①的结论求ab+bc+ac的最大值.
(二)已知a,b,x,y∈R+,
①求证:
+
≥
.
②利用①的结论求
+
(0<x<
)的最小值.
①求证:a2+b2+c2≥ab+bc+ac;
②若a+b+c=1,利用①的结论求ab+bc+ac的最大值.
(二)已知a,b,x,y∈R+,
①求证:
| x2 |
| a |
| y2 |
| b |
| (x+y)2 |
| a+b |
②利用①的结论求
| 1 |
| 2x |
| 9 |
| 1-2x |
| 1 |
| 2 |
分析:(一)①从不等式的左边入手,左边对应的代数式的二倍,分别写成两两相加的形式,在三组相加的式子中分别用均值不等式,整理成最简形式,得到右边的2倍,两边同时除以2,得到结果.
②由①得1=(a+b+c)2=a2+b2+c2+2(ab+bc+ac)≥3(ab+bc+ac)从而求出ab+bc+ac的最大值;
(二)①利用分析法进行证明.要证
+
≥
,只要证(
+
)(a+b)≥(x+y)2左边展开利用基本不等式证明即可;
②由①的结论知:
+
≥
=16,从而求出最大值.
②由①得1=(a+b+c)2=a2+b2+c2+2(ab+bc+ac)≥3(ab+bc+ac)从而求出ab+bc+ac的最大值;
(二)①利用分析法进行证明.要证
| x2 |
| a |
| y2 |
| b |
| (x+y)2 |
| a+b |
| x2 |
| a |
| y2 |
| b |
②由①的结论知:
| 1 |
| 2x |
| 9 |
| 1-2x |
| (1+3)2 |
| 2x+1-2x |
解答:证明:(一)①a2+b2≥2ab,c2+b2≥2bc,a2+c2≥2ac,…(3分)
三式相加可得a2+b2+c2≥ab+bc+ac
当且仅当a=b=c时等号成立 …(6分)
②1=(a+b+c)2=a2+b2+c2+2(ab+bc+ac)≥3(ab+bc+ac)…(9分)
则ab+bc+ac≤
,当且仅当a=b=c时等号成立. …(12分)
(二)①要证
+
≥
,只要证(
+
)(a+b)≥(x+y)2,…(3分)
则(
+
)(a+b)=x2+y2+
+
≥x2+y2+2xy=(x+y)2,
当且仅当bx=ay时等号成立.故原不等式得证. …(6分)
②由①的结论知:
+
≥
=16,
当且仅当x=
时,等号成立. …(12分)
三式相加可得a2+b2+c2≥ab+bc+ac
当且仅当a=b=c时等号成立 …(6分)
②1=(a+b+c)2=a2+b2+c2+2(ab+bc+ac)≥3(ab+bc+ac)…(9分)
则ab+bc+ac≤
| 1 |
| 3 |
(二)①要证
| x2 |
| a |
| y2 |
| b |
| (x+y)2 |
| a+b |
| x2 |
| a |
| y2 |
| b |
则(
| x2 |
| a |
| y2 |
| b |
| bx2 |
| a |
| ay2 |
| b |
当且仅当bx=ay时等号成立.故原不等式得证. …(6分)
②由①的结论知:
| 1 |
| 2x |
| 9 |
| 1-2x |
| (1+3)2 |
| 2x+1-2x |
当且仅当x=
| 1 |
| 8 |
点评:本题考查均值不等式的应用,考查不等式的证明方法,是一个基础题,这种题目常常考虑分拆后利用基本不等式,因为题目分拆后才符合均值不等式的表现形式.

练习册系列答案
相关题目
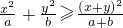 .
. 的最小值.
的最小值.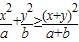 .
. 的最小值.
的最小值.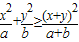 .
.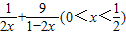 的最小值.
的最小值.