题目内容
1.设f(x)=$\frac{1+cos2x+sin2x}{\sqrt{2}sin(\frac{π}{2}+x)}$+asin(x+$\frac{π}{4}$)的最大值为3,则常数a=( )| A. | 1 | B. | a=1或a=-5 | C. | a=-1或a=1 | D. | a=±$\sqrt{7}$ |
分析 利用二倍角公式以及两角和与差的三角函数,化简函数的表达式,通过三角函数的最值列出方程求解即可.
解答 解:f(x)=$\frac{2{cos}^{2}x+2sinxcosx}{\sqrt{2}cosx}$+asin(x+$\frac{π}{4}$)=$\sqrt{2}$cosx+$\sqrt{2}$sinx+asin(x+$\frac{π}{4}$)
=2sin(x+$\frac{π}{4}$)+asin(x+$\frac{π}{4}$)=(2+a)sin(x+$\frac{π}{4}$),
则:|a+2|=3,∴a=1或a=-5.
故选:B.
点评 本题考查二倍角公式以及两角和与差的三角函数,考查计算能力.

练习册系列答案
相关题目
6.如果执行如图的程序框图,那么输出的值是( )
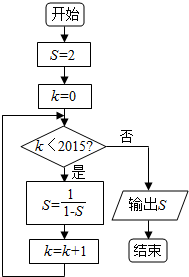

| A. | 2015 | B. | -1 | C. | $\frac{1}{2}$ | D. | 2 |
13.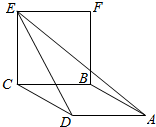 如图,四边形ABCD为菱形,四边形CEFB为正方形,平面ABCD⊥平面CEFB,CE=1,∠BCD=60°,若二面角D-CE-F的大小为α,异面直线BC与AE所成角的大小为β,则( )
如图,四边形ABCD为菱形,四边形CEFB为正方形,平面ABCD⊥平面CEFB,CE=1,∠BCD=60°,若二面角D-CE-F的大小为α,异面直线BC与AE所成角的大小为β,则( )
 如图,四边形ABCD为菱形,四边形CEFB为正方形,平面ABCD⊥平面CEFB,CE=1,∠BCD=60°,若二面角D-CE-F的大小为α,异面直线BC与AE所成角的大小为β,则( )
如图,四边形ABCD为菱形,四边形CEFB为正方形,平面ABCD⊥平面CEFB,CE=1,∠BCD=60°,若二面角D-CE-F的大小为α,异面直线BC与AE所成角的大小为β,则( )| A. | tanα=$\sqrt{3}$,tanβ=$\frac{\sqrt{7}}{3}$ | B. | tanα=$\frac{\sqrt{7}}{3}$,tanβ=$\sqrt{3}$ | ||
| C. | tanα=$\frac{2\sqrt{3}}{3}$,tanβ=$\frac{\sqrt{6}}{3}$ | D. | tanα=$\frac{\sqrt{7}}{3}$,tanβ=$\frac{\sqrt{6}}{3}$ |