题目内容
各棱长为a的正三棱柱的六个顶点都在同一个球面上,则此球的表面积为
【答案】分析:球心在上下底面中心的连线的中点上,球半径既位球心到各顶点的距离,找出球半径和a的关系再代入球的面积计算公式即可.
解答: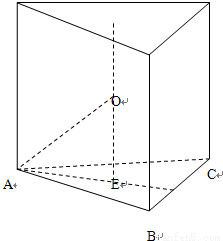 解:∵正三棱柱的六个顶点都在同一个球面上,
解:∵正三棱柱的六个顶点都在同一个球面上,
所以球心在上下底面中心的连线的中点上,
AB=a,OA=R,在△OEA中,OE=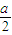 ,AE=
,AE=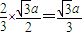 ,
,
∵AO2=OE2+AE2,
∴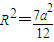 ,
,
∴球的表面积为4πR2=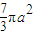 ,
,
故答案为 .
.
点评:本题以三棱柱为依托,考查了空间想象能力,逻辑推理能力和运算求解能力,是知识考查与能力考查并重的基础性试题
解答:
 解:∵正三棱柱的六个顶点都在同一个球面上,
解:∵正三棱柱的六个顶点都在同一个球面上,所以球心在上下底面中心的连线的中点上,
AB=a,OA=R,在△OEA中,OE=
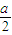 ,AE=
,AE=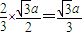 ,
,∵AO2=OE2+AE2,
∴
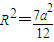 ,
,∴球的表面积为4πR2=
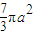 ,
,故答案为
 .
.点评:本题以三棱柱为依托,考查了空间想象能力,逻辑推理能力和运算求解能力,是知识考查与能力考查并重的基础性试题

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目