题目内容
已知动点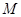 到点
到点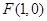 的距离,等于它到直线
的距离,等于它到直线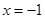 的距离.
的距离.
(1)求点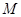 的轨迹
的轨迹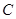 的方程;
的方程;
(2)过点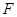 任意作互相垂直的两条直线
任意作互相垂直的两条直线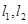 ,分别交曲线
,分别交曲线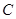 于点
于点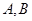 和
和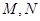 .
.
设线段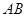 ,
,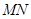 的中点分别为
的中点分别为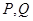 ,求证:直线
,求证:直线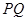 恒过一个定点;
恒过一个定点;
(3)在(2)的条件下,求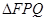 面积的最小值
面积的最小值
【答案】
(Ⅰ)设动点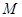 的坐标为
的坐标为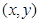 ,由题意得,
,由题意得, ,
,
化简得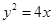 ,所以点
,所以点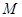 的轨迹
的轨迹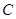 的方程为
的方程为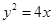 .
.
(Ⅱ)设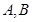 两点坐标分别为
两点坐标分别为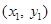 ,
,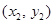 ,则点
,则点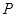 的坐标为
的坐标为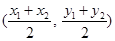 .由题意可设直线
.由题意可设直线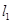 的方程为
的方程为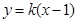
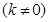 ,
,
由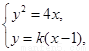 得
得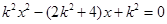 .
.
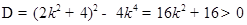 .
.
因为直线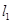 与曲线
与曲线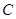 于
于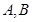 两点,所以
两点,所以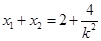 ,
,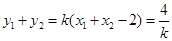 .所以点
.所以点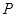 的坐标为
的坐标为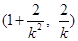 .
.
由题知,直线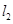 的斜率为
的斜率为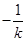 ,同理可得点
,同理可得点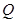 的坐标为
的坐标为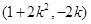 .
.
当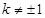 时,有
时,有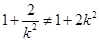 ,此时直线
,此时直线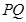 的斜率
的斜率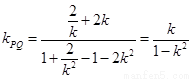 .
.
所以,直线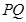 的方程为
的方程为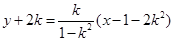 ,
,
整理得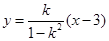 .于是,直线
.于是,直线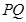 恒过定点
恒过定点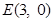 ;
;
当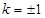 时,直线
时,直线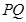 的方程为
的方程为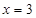 ,也过点
,也过点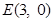 .
.
综上所述,直线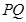 恒过定点
恒过定点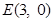 .
.
(Ⅲ)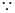
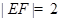 ,
,
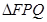 面积
面积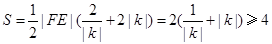 .
.
当且仅当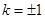 时,“
时,“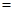 ”成立,所以
”成立,所以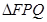 面积的最小值为
面积的最小值为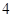 .
.
【解析】略

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
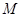 到点
到点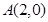 的距离等于它到直线
的距离等于它到直线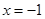 的距离,则点
的距离,则点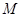 到点
到点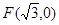 的距离与到直线
的距离与到直线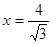 的距离之比为定值
的距离之比为定值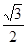 ,记
,记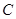 .
.
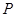 是圆
是圆 上第一象限内的任意一点,过
上第一象限内的任意一点,过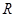 ,
,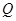 两点.
两点.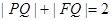 ;
;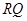 的最大值.
的最大值.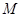 到点
到点
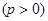 的距离比它到
的距离比它到 轴的距离多
轴的距离多 ·
· ,过点
,过点 的直线
的直线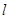 与曲线
与曲线 两点,若
两点,若 使得
使得 是以
是以