题目内容
已知函数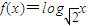 ,且数列{f(an)}是首项为2,公差为2的等差数列.
,且数列{f(an)}是首项为2,公差为2的等差数列.(1)求证:数列{an}是等比数列;
(2)设bn=an•f(an),求数列{bn}的前n项和Sn的最小值..
【答案】分析:(1)根据函数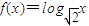 ,且数列{f(an)}是首项为2,公差为2的等差数列,可得
,且数列{f(an)}是首项为2,公差为2的等差数列,可得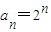 ,从而可得数列{an}是等比数列;
,从而可得数列{an}是等比数列;
(2)写出通项,利用错位相减法求和,确定其单调性,即可求得数列{bn}的前n项和Sn的最小值.
解答:(1)证明:∵函数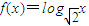 ,且数列{f(an)}是首项为2,公差为2的等差数列.
,且数列{f(an)}是首项为2,公差为2的等差数列.
∴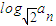 =2+(n-1)×2=2n
=2+(n-1)×2=2n
∴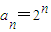
∵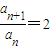
∴数列{an}是等比数列;(7分)
(2)解:由(1)知,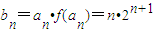 .…(8分)
.…(8分)
∴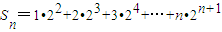 ,①
,①
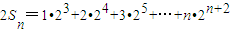 ②…(10分)
②…(10分)
②-①,得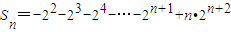 =
=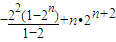
∴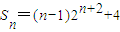 …(12分)
…(12分)
∵Sn+1-Sn=(n+1)×2n+2>0
∴{Sn}是递增数列,所以Sn的最小值等于S1=4…(14分)
点评:本题考查等比数列的证明,考查错位相减法求数列的和,考查单调性,解题的关键是确定数列的通项,属于中档题.
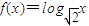 ,且数列{f(an)}是首项为2,公差为2的等差数列,可得
,且数列{f(an)}是首项为2,公差为2的等差数列,可得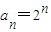 ,从而可得数列{an}是等比数列;
,从而可得数列{an}是等比数列;(2)写出通项,利用错位相减法求和,确定其单调性,即可求得数列{bn}的前n项和Sn的最小值.
解答:(1)证明:∵函数
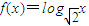 ,且数列{f(an)}是首项为2,公差为2的等差数列.
,且数列{f(an)}是首项为2,公差为2的等差数列.∴
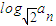 =2+(n-1)×2=2n
=2+(n-1)×2=2n∴
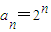
∵
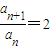
∴数列{an}是等比数列;(7分)
(2)解:由(1)知,
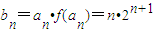 .…(8分)
.…(8分)∴
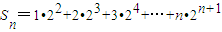 ,①
,①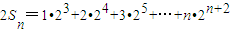 ②…(10分)
②…(10分)②-①,得
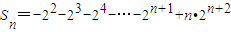 =
=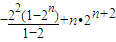
∴
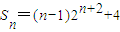 …(12分)
…(12分)∵Sn+1-Sn=(n+1)×2n+2>0
∴{Sn}是递增数列,所以Sn的最小值等于S1=4…(14分)
点评:本题考查等比数列的证明,考查错位相减法求数列的和,考查单调性,解题的关键是确定数列的通项,属于中档题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
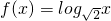 ,且数列{f(an)}是首项为2,公差为2的等差数列.
,且数列{f(an)}是首项为2,公差为2的等差数列.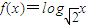 ,且数列{f(an)}是首项为2,公差为2的等差数列.
,且数列{f(an)}是首项为2,公差为2的等差数列.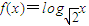 ,且数列{f(an)}是首项为2,公差为2的等差数列.
,且数列{f(an)}是首项为2,公差为2的等差数列.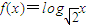 ,且数列{f(an)}是首项为2,公差为2的等差数列.
,且数列{f(an)}是首项为2,公差为2的等差数列.