题目内容
函数f(x)对任意x∈R都有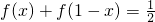 成立.
成立.
(Ⅰ)求和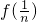
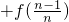 (n∈N*)的值;
(n∈N*)的值;
(Ⅱ)数列{an}满足条件;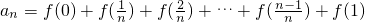 ,试证:数列{an}是等差数列.
,试证:数列{an}是等差数列.
解:(Ⅰ)∵f(x)对任意x∈R都有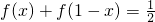 成立
成立
∴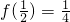 ,令
,令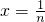 ,则有
,则有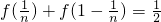 ,即
,即
(Ⅱ)∵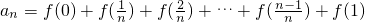
∴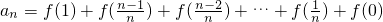
两式相加可得,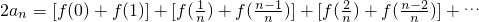
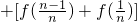
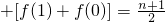 .
.
所以数列{an} 是等差数列.
分析:(Ⅰ)由f(x)对任意x∈R都有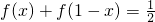 成立可令
成立可令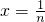 ,则可求
,则可求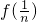
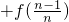
(Ⅱ)由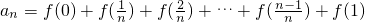 可得
可得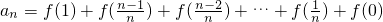 ,利用倒序相加可求an,进而可证数列{an} 是等差数列.
,利用倒序相加可求an,进而可证数列{an} 是等差数列.
点评:本题主要考查了利用赋值求抽象函数的函数值及利用倒序相加求解数列的和的方法的应用,要注意该方法是推倒等差数列的求和公式的方法.
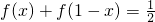 成立
成立∴
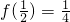 ,令
,令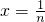 ,则有
,则有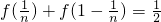 ,即
,即
(Ⅱ)∵
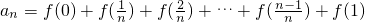
∴
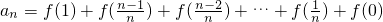
两式相加可得,
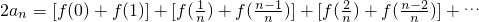
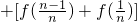
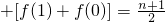 .
.所以数列{an} 是等差数列.
分析:(Ⅰ)由f(x)对任意x∈R都有
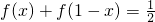 成立可令
成立可令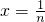 ,则可求
,则可求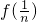
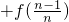
(Ⅱ)由
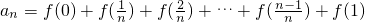 可得
可得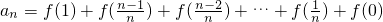 ,利用倒序相加可求an,进而可证数列{an} 是等差数列.
,利用倒序相加可求an,进而可证数列{an} 是等差数列.点评:本题主要考查了利用赋值求抽象函数的函数值及利用倒序相加求解数列的和的方法的应用,要注意该方法是推倒等差数列的求和公式的方法.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目