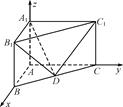
题目内容
如图,三棱柱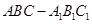 中,△ABC是正三角形,
中,△ABC是正三角形,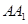
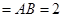 ,平面
,平面 平面
平面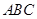 ,
,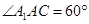 .
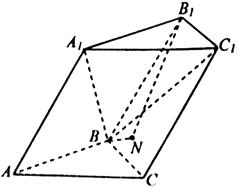
.
(1)证明: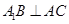 ;
;
(2)证明:求二面角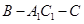 的余弦值;
的余弦值;
(3)设点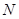 是平面
是平面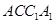 内的动点,求
内的动点,求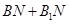 的最小值.
的最小值.
(1)证明过程详见试题解析;(2) ;(3)
;(3) .
.
解析试题分析:(1)如图,取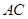 的中点
的中点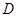 ,连结
,连结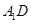 、
、 ,
,
因为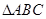 是正三角形,所以
是正三角形,所以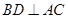 ,又因为
,又因为 ,所以
,所以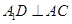 ;由
;由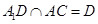 ,那么
,那么 ,所以
,所以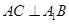 ;(2)由(1)结合条件可以得到
;(2)由(1)结合条件可以得到 就是二面角
就是二面角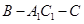 的平面角,在直角三角形
的平面角,在直角三角形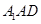 中,有
中,有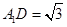 ,又
,又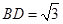 那么在直角三角形
那么在直角三角形 中,可根据勾股定理求出
中,可根据勾股定理求出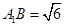 ,那么
,那么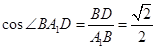 ;(3)以
;(3)以 为坐标原点建立直角平面坐标系,要使得
为坐标原点建立直角平面坐标系,要使得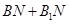 最小,就是要找出点
最小,就是要找出点 关于平面
关于平面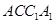 的对称点
的对称点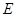 ,求出
,求出 即可.因此建立如解析中空间直角坐标系求.
即可.因此建立如解析中空间直角坐标系求.
试题解析:(1)证明:∵  ,△
,△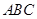 是正三角形,
是正三角形,
∴ 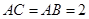 ,
,
∴  ,
,
又∵ 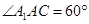 ,∴△
,∴△ 是正三角形,
是正三角形,
取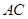 中点
中点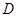 ,连结
,连结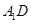 、
、 ,则
,则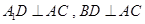
又∵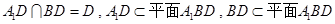 ,
,
∴ ,
,
又∵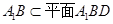 ,
,
∴ 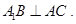
(2)证明:∵ ,由(1)知
,由(1)知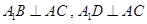 ,
,
∴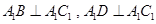 ,
,
∴ ;
;
∵ 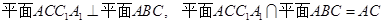
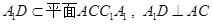 ∴
∴
∵ ,∴
,∴ 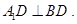 ,
,
在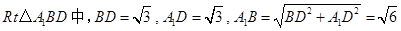
∴ 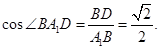
(3)解:延长 至
至 使
使 ,连结
,连结 、
、 、
、 ,
,
以 为原点建立如图所示的空间直角坐标系,
为原点建立如图所示的空间直角坐标系,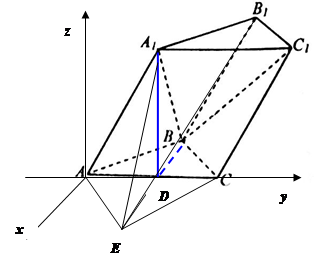
则点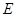 的坐标为
的坐标为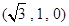 ,
,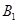 的坐标是
的坐标是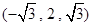 ,
,
则 就是
就是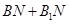 的最小值,
的最小值,
考点:立体几何中的垂直问题;成角问题;距离问题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
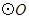 的直径
的直径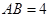 ,点
,点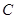 、
、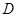 为
为 ,
,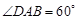 ,
,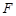 为弧
为弧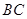 的中点.将
的中点.将 折起,使两个半圆所在平面互相垂直(如图2).
折起,使两个半圆所在平面互相垂直(如图2).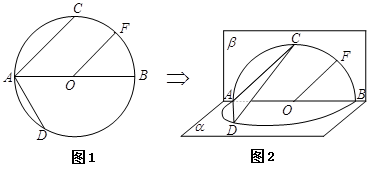
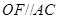 ;
;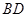 上是否存在点
上是否存在点 ,使得
,使得 平面
平面 ?若存在,试指出点
?若存在,试指出点 的正弦值.
的正弦值.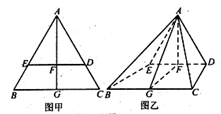
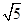 ,AB=AD=
,AB=AD=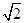 .将图(1)沿直线BD折起,使得二面角ABDC为60°,如图(2).
.将图(1)沿直线BD折起,使得二面角ABDC为60°,如图(2).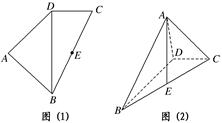
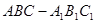 ,底面
,底面 中
中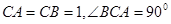 ,棱
,棱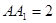 ,
,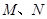 分别为
分别为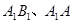 的中点.
的中点.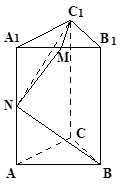
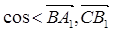 >的值;
>的值;

 AB.
AB. 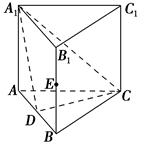
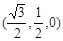 ,D点在平面yoz上,BC=2,∠BDC=90°,∠DCB=30°.
,D点在平面yoz上,BC=2,∠BDC=90°,∠DCB=30°.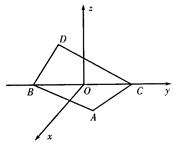
 的值.
的值.