题目内容
已知函数f(x)= sin 2x-cos2x-
sin 2x-cos2x- ,x∈R.
,x∈R.
(1)求函数f(x)的最小值和最小正周期;
(2)设△ABC的内角A、B、C的对边分别为a、b、c,且c= ,f(C)=0,若sin B=2sin A,求a,b的值.
,f(C)=0,若sin B=2sin A,求a,b的值.
 sin 2x-cos2x-
sin 2x-cos2x- ,x∈R.
,x∈R.(1)求函数f(x)的最小值和最小正周期;
(2)设△ABC的内角A、B、C的对边分别为a、b、c,且c=
 ,f(C)=0,若sin B=2sin A,求a,b的值.
,f(C)=0,若sin B=2sin A,求a,b的值.(1)-2 π (2)a=1且b=2
(1)f(x)= sin 2x-
sin 2x- -
- =sin(2x-
=sin(2x- )-1,则f(x)的最小值是-1-1=-2,且f(x)的最小正周期T=
)-1,则f(x)的最小值是-1-1=-2,且f(x)的最小正周期T= =π.
=π.
(2)f(C)=sin(2C- )-1=0,则sin(2C-
)-1=0,则sin(2C- )=1.
)=1.
∵0<C<π,
∴- <2C-
<2C- <
< π,因此2C-
π,因此2C- =
= ,∴C=
,∴C= .
.
∵sin B=2sin A及正弦定理,得b=2a.①
由余弦定理,得c2=a2+b2-2abcos ,且c=
,且c= ,
,
∴a2+b2-ab=3,②
由①②联立,得a=1且b=2.
 sin 2x-
sin 2x- -
- =sin(2x-
=sin(2x- )-1,则f(x)的最小值是-1-1=-2,且f(x)的最小正周期T=
)-1,则f(x)的最小值是-1-1=-2,且f(x)的最小正周期T= =π.
=π.(2)f(C)=sin(2C-
 )-1=0,则sin(2C-
)-1=0,则sin(2C- )=1.
)=1.∵0<C<π,
∴-
 <2C-
<2C- <
< π,因此2C-
π,因此2C- =
= ,∴C=
,∴C= .
.∵sin B=2sin A及正弦定理,得b=2a.①
由余弦定理,得c2=a2+b2-2abcos
 ,且c=
,且c= ,
,∴a2+b2-ab=3,②
由①②联立,得a=1且b=2.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 +α)=
+α)= ,则cos(
,则cos( -2α)等于( )
-2α)等于( )
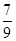
 (
( ).
). 的最小正周期及
的最小正周期及 上的值域;
上的值域; 中,
中, ,
, .若
.若 ,求
,求 为锐角,且cos
为锐角,且cos =
= cos
cos  =
=  , 则cos
, 则cos =_________
=_________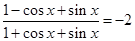 ,则
,则 的值为( )
的值为( )



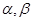 为锐角,
为锐角, 则
则 .
. 满足
满足 ,则
,则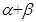 等于( )
等于( )


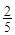 ,tan(α+
,tan(α+ )=
)= , 那么tan(β-
, 那么tan(β-



 ,则
,则 = ( )
= ( )


