题目内容
以下命题:
①如果向量 与任何向量不能构成空间向量的一组基底,那么
与任何向量不能构成空间向量的一组基底,那么 的关系是不共线;
的关系是不共线;
② 为空间四点,且向量
为空间四点,且向量 不构成空间的一个基底,那么点
不构成空间的一个基底,那么点 一定共面;③已知向量
一定共面;③已知向量 是空间的一个基底,则向量
是空间的一个基底,则向量 也是空间的一个基底.
也是空间的一个基底.
其中正确的命题是( )
| A.①② | B.①③ | C.②③ | D.①②③ |
C
解析试题分析:①如果向量 与任何向量不能构成空间向量的一组基底,那么
与任何向量不能构成空间向量的一组基底,那么 的关系是共线向量,故此项错;②因为若点
的关系是共线向量,故此项错;②因为若点 不共面,则向量
不共面,则向量 可构成空间的一个基底,因而此命题正确; ③:已知向量
可构成空间的一个基底,因而此命题正确; ③:已知向量 是空间的一个基底,则向量
是空间的一个基底,则向量 也是空间的一个基底.因为三个向量非零不共线,正确.
也是空间的一个基底.因为三个向量非零不共线,正确.
故选C.
因为向量 是空间的一个基底,那么
是空间的一个基底,那么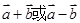 可能与向量
可能与向量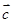 共线,因而向量
共线,因而向量 不一定是空间的一个基底,错;故正确的命题有
不一定是空间的一个基底,错;故正确的命题有
考点:共线向量与共面向量.
点评:有关空间向量的命题直接判断错误时,可以考虑举反例论证.

练习册系列答案
相关题目
已知空间四边形ABCD中,G为CD的中点,则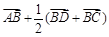 等于( )
等于( )
A.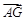 | B. | C. | D. |
设 是两个非零向量,则下列结论不正确的是
是两个非零向量,则下列结论不正确的是
A.若存在一个实数 满足 满足 ,则 ,则 与 与 共线 共线 |
B.若 ,则 ,则 |
C.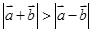 |
D.若 与 与 为两个方向相同的向量,则 为两个方向相同的向量,则 |
如图.点M是 的重心,则
的重心,则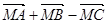 为( )
为( ) 
A. | B.4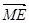 | C.4 | D.4 |
已知 =(5,-3),C(-1,3),
=(5,-3),C(-1,3), =2
=2 ,则点D的坐标为
,则点D的坐标为
| A.(11,9) | B.(4,0) | C.(9,3) | D.(9,-3) |
 = ( )
= ( )








 ,
, ,
, .若
.若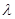 为实数,
为实数, ,则
,则 。
。 不共线,若
不共线,若 ,且A、B、C三点共线,则关于实数
,且A、B、C三点共线,则关于实数 一定成立的关系式为( )
一定成立的关系式为( ) ="1" B.
="1" B. =" -1" C.
=" -1" C. ="1" D.
="1" D. =1
=1