题目内容
20．函数f（x）=cos（x+2φ）+2sinφsin（x+φ）的最大值为1．分析 由条件利用两角和差的余弦公式把函数f（x）的解析式化为cosx，再利用余弦函数的值域求得它的最大值．
解答 解：∵函数f（x）=cos（x+2φ）+2sinφsin（x+φ）=cos（x+φ）cosφ-sin（x+φ）sinφ+2sinφsin（x+φ）
=cos（x+φ）cosφ+sin（x+φ）sinφ=cos（x+φ-φ）=cosx，
故函数f（x）的最大值为1．
点评 本题主要考查两角和差的余弦公式，余弦函数的值域，属于基础题．
练习册系列答案
相关题目
10．已知x，y∈R，则“x2+y2＜1”是“xy+1＞x+y”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
11．若方程|2x-3|+m=0有两个不同实数根，则实数m的取值范围是（ ）
| A． | （-3，0） | B． | （-∞，0） | C． | （0，3） | D． | （-3，3） |
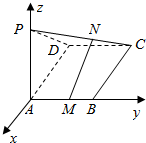已知PA垂直于正方形ABCD所在的平面，M，N分别在AB，PC上，且PN=2NC，AM=2MB，PA=AD=1，如图建立空间直角坐标系，求$\overrightarrow{MN}$的坐标．
已知过点A（-1，0）的动直线l与圆C：x2+（y-3）2=4相交于P、Q两点，M是PQ中点，l与直线m：x+3y+6=0相交于N．