题目内容
(
南通一中模拟)已知f(x)是定义在[-1,1]上的奇函数,且f(1)=1,若m、n [-1,1],m+n≠0时,
[-1,1],m+n≠0时, .
.
(1)
用定义证明函数f(x)在[-1,1]上是增函数;(2)
解不等式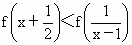 ;
;
(3)
若 对所有x
对所有x [-1,1],a
[-1,1],a [-2,2]恒成立,求实数t的取值范围.
[-2,2]恒成立,求实数t的取值范围.
答案:略
解析:
解析:
|
解析: (1)证明:任取 ,且 ,且 , , , ,
则  , ,
∵  , ,
∴  ,由已知 ,由已知 ,又 ,又 , ,
∴  ,即f(x)在[-1,1]上为增函数. (4分) ,即f(x)在[-1,1]上为增函数. (4分)
(2) ∵f(x)在[-1,1]上为增函数,∴  解得 解得 . (9分) . (9分)
(3) 由(1)可知f(x)在[-1,1]上为增函数,且f(1)=1,故对x [-1,1],恒有 [-1,1],恒有 , ,
所以要使 即要 记 解得 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 对所有x
对所有x 成立,故
成立,故 ,
, ,对a
,对a ,只需g(a)在[-2,2]上的最小值大于等于0,
,只需g(a)在[-2,2]上的最小值大于等于0, ,
, ,
, 或
或 或t=0.∴t的取值范围是
或t=0.∴t的取值范围是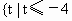 或t≥4或t=0} (15分)
或t≥4或t=0} (15分) .
.
 ,设向量a=(sinx,2),
,设向量a=(sinx,2),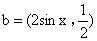 ,c=(cos 2x,1),d=(1,2).当x
,c=(cos 2x,1),d=(1,2).当x [0,π]时,不等式f(a·b)>f(c·d)的解集为________.
[0,π]时,不等式f(a·b)>f(c·d)的解集为________. ,且
,且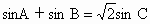 .△ABC的面积为
.△ABC的面积为 ,则角C的度数为________°.
,则角C的度数为________°. ,数列
,数列 满足
满足 .
.
 是等比数列;
是等比数列;
 取最大值,并求出最大值;
取最大值,并求出最大值;
 对任意
对任意 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.