题目内容
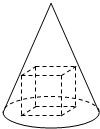
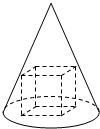 已知圆锥的母线长与底面半径长之比为3:1,一个正方体有四个顶点在圆锥的底面内,另外的四个顶点在圆锥的侧面上(如图),则圆锥与正方体的表面积之比为( )
已知圆锥的母线长与底面半径长之比为3:1,一个正方体有四个顶点在圆锥的底面内,另外的四个顶点在圆锥的侧面上(如图),则圆锥与正方体的表面积之比为( )| A、π:1 | B、3π:1 | C、3π:2 | D、3π:4 |
分析:根据几何体作出轴截面,由图和题意列出圆锥的半径和正方体棱长的关系式,求出它们的长度关系,再代入对应的面积公式,求出表面积的比值.
解答: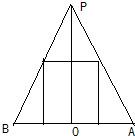 解:作出几何体的轴截面如图:
解:作出几何体的轴截面如图:
由题意设圆锥的底面半径为r,
则母线长l=3r,
则圆锥的高h=2
r,设正方体的棱长为a,
由轴截面得,
=
,即
=
,解得3a=2
r,
∴圆锥与正方体的表面积之比为(πr2+πrl):6a2=4πr2:6a2=3π:4,
故选D.
 解:作出几何体的轴截面如图:
解:作出几何体的轴截面如图:由题意设圆锥的底面半径为r,
则母线长l=3r,
则圆锥的高h=2
| 2 |
由轴截面得,
| h-a |
| h |
| ||
| 2r |
2
| ||
2
|
| ||
| 2r |
| 2 |
∴圆锥与正方体的表面积之比为(πr2+πrl):6a2=4πr2:6a2=3π:4,
故选D.
点评:本题的考点是由三视图求几何体的体积、表面积,需要由三视图判断空间几何体的结构特征,并根据三视图求出每个几何体中几何元素的长度,代入对应的体积以及面积公式分别求解,对于多面体需要把各个面的面积求和即它的表面积,考查了空间想象能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
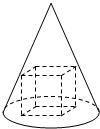 已知圆锥的母线长与底面半径长之比为3:1,一个正方体有四个顶点在圆锥的底面内,另外的四个顶点在圆锥的侧面上(如图),则圆锥与正方体的表面积之比为
已知圆锥的母线长与底面半径长之比为3:1,一个正方体有四个顶点在圆锥的底面内,另外的四个顶点在圆锥的侧面上(如图),则圆锥与正方体的表面积之比为