题目内容
第一题满分4分,第二题满分6分,第三题满分8分.已知椭圆C的长轴长是焦距的两倍,其左、右焦点依次为F1、F2,抛物线M:y2=4mx(m>0)的准线与x轴交于F1,椭圆C与抛物线M的一个交点为P.
(1)当m=1时,求椭圆C的方程;
(2)在(1)的条件下,直线l过焦点F2,与抛物线M交于A、B两点,若弦长|AB|等于△PF1F2的周长,求直线l的方程;
(3)是否存在实数m,使得△PF1F2的边长为连续的自然数.
【答案】分析:(1)因为椭圆C的长轴长是焦距的两倍,所以可求出a,b的关系,当m=1时,可知抛物线的方程,进而求出抛物线的准线方程,因为抛物线M:y2=4mx(m>0)的准线与x轴交于F1,所以可以得到c的值,再根据椭圆中a,b,c的关系,即可求出椭圆方程.
(2)设出直线l的点斜式方程,与椭圆方程联立,利用弦长公式求出弦|AB|的长,因为弦长|AB|等于△PF1F2的周长,
可求出直线l的斜率,进而求出直线l的方程.
(3)先假设存在实数m,使得△PF1F2的边长为连续的自然数.则可用含m的方程表示椭圆与抛物线,联立,解得P点坐标,利用焦半径公式求出△PF1F2的三边长,再根据假设求m,若能求出,则假设正确,若求不出,则假设不正确.
解答:解:(1)设椭圆的实半轴长为a,短半轴长为b,半焦距为c,
当m=1时,由题意得,a=2c=2,b2=a2-c2=3,a2=4,
所以椭圆的方程为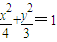 .
.
(2)依题意知直线l的斜率存在,设l:y=k(x-1),由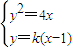 得,k2x2-(2k2+4)x+k2=0,由直线l与抛物线M有两个交点,可知k≠0.设A(x1,y1),B(x2,y2),由韦达定理得
得,k2x2-(2k2+4)x+k2=0,由直线l与抛物线M有两个交点,可知k≠0.设A(x1,y1),B(x2,y2),由韦达定理得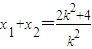 ,则
,则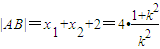 (6分)又△PF1F2的周长为2a+2c=6,所以
(6分)又△PF1F2的周长为2a+2c=6,所以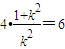 ,
,
解得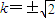 ,从而可得直线l的方程为
,从而可得直线l的方程为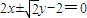
(3)假设存在满足条件的实数m,
由题意得c=m,a=2m⇒b2=3m2,所以椭圆C的方程为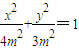
联立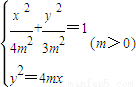 解得
解得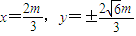 即
即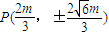 .
.
所以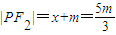 ,
,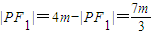 ,|F1F2|=2m,
,|F1F2|=2m,
即△PF1F2的边长分别为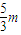 、
、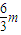 、
、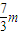 ,显然|PF2|<|F1F2|<|PF1|,
,显然|PF2|<|F1F2|<|PF1|,
所以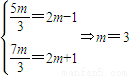 ,故当m=3时,使得△PF1F2的边长为连续的自然数.
,故当m=3时,使得△PF1F2的边长为连续的自然数.
点评:本题主要考查了椭圆方程的求法,直线与椭圆位置关系的判断.
(2)设出直线l的点斜式方程,与椭圆方程联立,利用弦长公式求出弦|AB|的长,因为弦长|AB|等于△PF1F2的周长,
可求出直线l的斜率,进而求出直线l的方程.
(3)先假设存在实数m,使得△PF1F2的边长为连续的自然数.则可用含m的方程表示椭圆与抛物线,联立,解得P点坐标,利用焦半径公式求出△PF1F2的三边长,再根据假设求m,若能求出,则假设正确,若求不出,则假设不正确.
解答:解:(1)设椭圆的实半轴长为a,短半轴长为b,半焦距为c,
当m=1时,由题意得,a=2c=2,b2=a2-c2=3,a2=4,
所以椭圆的方程为
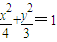 .
.(2)依题意知直线l的斜率存在,设l:y=k(x-1),由
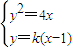 得,k2x2-(2k2+4)x+k2=0,由直线l与抛物线M有两个交点,可知k≠0.设A(x1,y1),B(x2,y2),由韦达定理得
得,k2x2-(2k2+4)x+k2=0,由直线l与抛物线M有两个交点,可知k≠0.设A(x1,y1),B(x2,y2),由韦达定理得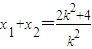 ,则
,则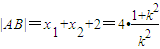 (6分)又△PF1F2的周长为2a+2c=6,所以
(6分)又△PF1F2的周长为2a+2c=6,所以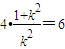 ,
,解得
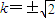 ,从而可得直线l的方程为
,从而可得直线l的方程为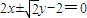
(3)假设存在满足条件的实数m,
由题意得c=m,a=2m⇒b2=3m2,所以椭圆C的方程为
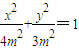
联立
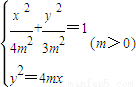 解得
解得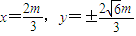 即
即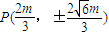 .
.所以
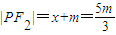 ,
,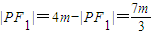 ,|F1F2|=2m,
,|F1F2|=2m,即△PF1F2的边长分别为
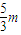 、
、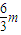 、
、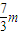 ,显然|PF2|<|F1F2|<|PF1|,
,显然|PF2|<|F1F2|<|PF1|,所以
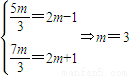 ,故当m=3时,使得△PF1F2的边长为连续的自然数.
,故当m=3时,使得△PF1F2的边长为连续的自然数.点评:本题主要考查了椭圆方程的求法,直线与椭圆位置关系的判断.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 相切。
相切。 的直线与曲线M相交于A,B两点,A,B在直线
的直线与曲线M相交于A,B两点,A,B在直线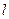 上的射影是
上的射影是 。求梯形
。求梯形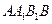 的面积;
的面积;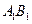 上的动点,当△ABC为直角三角形时,求点C的坐标。
上的动点,当△ABC为直角三角形时,求点C的坐标。 克牌洗匀后,背面朝上放在桌面上,甲先抽,乙后抽,抽出的牌不放回,各抽一张。
克牌洗匀后,背面朝上放在桌面上,甲先抽,乙后抽,抽出的牌不放回,各抽一张。 分别表示甲、乙抽到的牌的数字(方片4用4’表示,红桃2,红
分别表示甲、乙抽到的牌的数字(方片4用4’表示,红桃2,红 桃3,红桃4分别用2,3,4表示),写出甲乙二人抽
桃3,红桃4分别用2,3,4表示),写出甲乙二人抽 到的牌的所有情况;
到的牌的所有情况; 乙大,则甲胜;若甲抽到的牌的牌面数字不比乙大,则乙胜。你认为此游
乙大,则甲胜;若甲抽到的牌的牌面数字不比乙大,则乙胜。你认为此游 戏是否公平,说明你的理由。
戏是否公平,说明你的理由。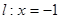 相切。
相切。 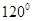 的直线与曲线M相交于A,B两点,A,B在直线
的直线与曲线M相交于A,B两点,A,B在直线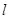 上的射影是
上的射影是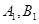 。求梯形
。求梯形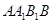 的面积;
的面积;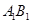 上的动点,当△ABC为直角三角形时,求点C的坐标。
上的动点,当△ABC为直角三角形时,求点C的坐标。 分别表示甲、乙抽到的牌的数字(方片4用4’表示,红桃2,红桃3,红桃4分别用2,3,4表示),写出甲乙二人抽到的牌的所有情况;
分别表示甲、乙抽到的牌的数字(方片4用4’表示,红桃2,红桃3,红桃4分别用2,3,4表示),写出甲乙二人抽到的牌的所有情况;