题目内容
已知数列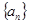 是各项均为正数的等比数列,且
是各项均为正数的等比数列,且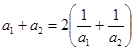 ,
,
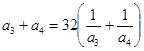 。
。
(I)求数列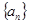 的通项公式;(II)设
的通项公式;(II)设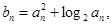 求数列
求数列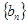 的前n项和Sn。
的前n项和Sn。
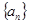 是各项均为正数的等比数列,且
是各项均为正数的等比数列,且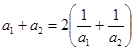 ,
,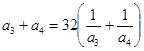 。
。(I)求数列
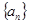 的通项公式;(II)设
的通项公式;(II)设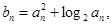 求数列
求数列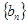 的前n项和Sn。
的前n项和Sn。(I)∵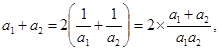
 ………………………………1分
………………………………1分
数列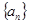 各项均为正数,
各项均为正数,
∴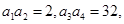 ………………………………………………………2分
………………………………………………………2分
∴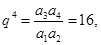 ∴
∴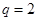 ……………………………4分
……………………………4分
又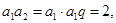 ∴
∴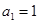 ………………………6分
………………………6分
∴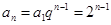 …………………7分
…………………7分
(II)∵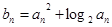 ∴
∴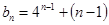 ……………8分
……………8分
∴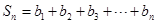
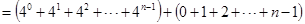 ……………10分
……………10分
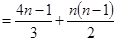
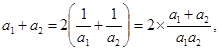
 ………………………………1分
………………………………1分数列
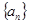 各项均为正数,
各项均为正数,∴
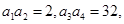 ………………………………………………………2分
………………………………………………………2分∴
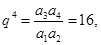 ∴
∴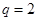 ……………………………4分
……………………………4分又
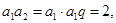 ∴
∴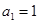 ………………………6分
………………………6分∴
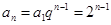 …………………7分
…………………7分(II)∵
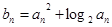 ∴
∴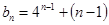 ……………8分
……………8分∴
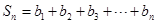
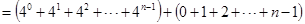 ……………10分
……………10分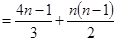
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
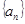 满足
满足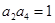 ,
,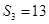 ,
,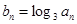 ,则数列
,则数列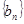 的前10项和是
的前10项和是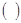



 为等差数列,且
为等差数列,且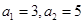 ,则
,则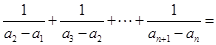 ( )
( )
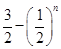
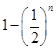
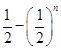
 中,
中, ,
, ,则
,则



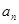 } 的各项都是正数,且
} 的各项都是正数,且 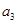
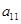 =16,则
=16,则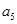 =( )
=( )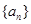 中,
中,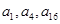 成等比数列,则
成等比数列,则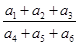 =
=  的各项均为正数,且
的各项均为正数,且 ,则
,则




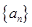 的各项均为正数,且
的各项均为正数,且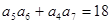 ,则
,则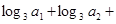
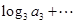
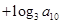 ( )
( )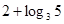
 中,
中, ,
, 9,则
9,则 ( )
( )
