题目内容
一种填数字彩票2元一张,购买者在彩票上依次填上0~9中的两个数字(允许重复),中奖规则如下:如果购买者所填的两个数字依次与开奖的四个有序数字分别对应相等,则中一等奖10元;如果购买者所填的两个数字中,只有第二个数字与开奖的第二个数字相等,则中二等奖2元,其他情况均不中奖.
(1)小明和小辉在没有商量的情况下各买了一张这种彩票,求他俩都中一等奖的概率;
(2)求购买一张这种彩票能够中奖的概率;
解:(1)由题意知本题是一个相互独立事件同时发生的概率,
小明中一等奖的概率是一个古典概型,
试验发生的所有事件由分步计数原理知共有10×10种结果,
满足条件的事件是1个,
小明(小辉)中一等奖的概率为P=0.01
由相互独立事件同时发生的概率公式得到
∴小明,小辉都中一等奖的概率为p=0.01×0.01=0.0001
(2)购买一张这种彩票能够中奖包括中一等奖或中二等奖,
购买一张这样的彩票:
中一等奖的概率为
中二等奖的概率为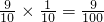
∵这两个事件是互斥事件.
∴购买一张彩票能中奖的概率为: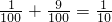 .
.
分析:(1)由题意知本题是一个相互独立事件同时发生的概率,小明中一等奖的概率是一个古典概型,试验发生的所有事件由分步计数原理知共有10×10种结果,满足条件的事件是1个,得到小明中一等奖的概率,由相互独立事件同时发生的概率公式得到结果.
(2)购买一张这种彩票能够中奖包括中一等奖或中二等奖,由第一问可知中一等奖的概率,算出中二等奖的概率,根据互斥事件的概率公式得到结果.
点评:本题包括古典概型,相互独立事件同时发生和互斥事件的概率,实际上古典概型是解题的基础,学好古典概型可以为其它概率的学习奠定基础,同时有利于理解概率的概念,有利于计算一些事件的概率,有利于解释生活中的一些问题.
小明中一等奖的概率是一个古典概型,
试验发生的所有事件由分步计数原理知共有10×10种结果,
满足条件的事件是1个,
小明(小辉)中一等奖的概率为P=0.01
由相互独立事件同时发生的概率公式得到
∴小明,小辉都中一等奖的概率为p=0.01×0.01=0.0001
(2)购买一张这种彩票能够中奖包括中一等奖或中二等奖,
购买一张这样的彩票:
中一等奖的概率为

中二等奖的概率为
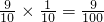
∵这两个事件是互斥事件.
∴购买一张彩票能中奖的概率为:
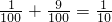 .
.分析:(1)由题意知本题是一个相互独立事件同时发生的概率,小明中一等奖的概率是一个古典概型,试验发生的所有事件由分步计数原理知共有10×10种结果,满足条件的事件是1个,得到小明中一等奖的概率,由相互独立事件同时发生的概率公式得到结果.
(2)购买一张这种彩票能够中奖包括中一等奖或中二等奖,由第一问可知中一等奖的概率,算出中二等奖的概率,根据互斥事件的概率公式得到结果.
点评:本题包括古典概型,相互独立事件同时发生和互斥事件的概率,实际上古典概型是解题的基础,学好古典概型可以为其它概率的学习奠定基础,同时有利于理解概率的概念,有利于计算一些事件的概率,有利于解释生活中的一些问题.

练习册系列答案
相关题目