题目内容
双曲线 的离心率
的离心率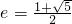 ,点A与F分别是双曲线的左顶点和右焦点,B(0,b),则∠ABF等于
,点A与F分别是双曲线的左顶点和右焦点,B(0,b),则∠ABF等于
- A.45°
- B.60°
- C.90°
- D.120°
C
分析:由离心率能够得出b2=ac,再根据题意得出|AF|=a+c|BF|=c,|AB|2=a2+b2,进而判断BF|2+|AB|2=|AF|2,从而得出
∠ABF等于90°.
解答:由题意知因为e= =
=
∴ =
=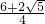 =
=
∴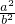 =
= =
=
∴b2=ac
∵|AF|=a+c|BF|=c,在直角三角形BOF中易得|BF|2=c2+b2
∴|AF|2=a2+2ac+c2|AB|2=a2+b2
又∵上面推出b^2=ac,
故|BF|2=c2+b2=c2+ac
显然|BF|2+|AB|2=|AF|2
∴∠ABF=90°
故选C.
点评:本题考查了椭圆的性质,由离心率能够得出b2=ac,是解题的关键,属于中档题.
分析:由离心率能够得出b2=ac,再根据题意得出|AF|=a+c|BF|=c,|AB|2=a2+b2,进而判断BF|2+|AB|2=|AF|2,从而得出
∠ABF等于90°.
解答:由题意知因为e=
 =
=
∴
 =
=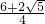 =
=
∴
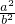 =
= =
=
∴b2=ac
∵|AF|=a+c|BF|=c,在直角三角形BOF中易得|BF|2=c2+b2
∴|AF|2=a2+2ac+c2|AB|2=a2+b2
又∵上面推出b^2=ac,
故|BF|2=c2+b2=c2+ac
显然|BF|2+|AB|2=|AF|2
∴∠ABF=90°
故选C.
点评:本题考查了椭圆的性质,由离心率能够得出b2=ac,是解题的关键,属于中档题.

练习册系列答案
相关题目
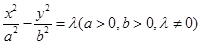 同一条渐近线上的两个不同的点,已知向量
同一条渐近线上的两个不同的点,已知向量 =(1,0),
=(1,0),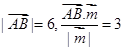 ,则双曲线的离心率e等于
,则双曲线的离心率e等于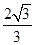 C.2或
C.2或 D. 2或
D. 2或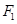 和
和 为双曲线
为双曲线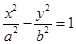 (
( )的两个焦点, 若点
)的两个焦点, 若点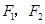 和点
和点 是正三角形的三个顶点,则双曲线的离心率为( )。
是正三角形的三个顶点,则双曲线的离心率为( )。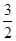 B.
B.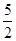 C.
C.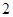 D.3
D.3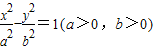 的离心率
的离心率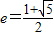 ,点A与F分别是双曲线的左顶点和右焦点,B(0,b),则∠ABF等于( )
,点A与F分别是双曲线的左顶点和右焦点,B(0,b),则∠ABF等于( )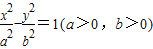 的离心率
的离心率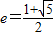 ,点A与F分别是双曲线的左顶点和右焦点,B(0,b),则∠ABF等于( )
,点A与F分别是双曲线的左顶点和右焦点,B(0,b),则∠ABF等于( )