Question

(9分）设x>0,y>0且x+y=1，求证：≥9.

 

Answer 1

【答案】

均值不等式的运用，利用一正二定三相等来求解最值。

【解析】

试题分析：证明:证法一（综合法）：（2+2+3+2=9）

左边.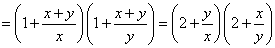

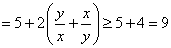证法二（分析法）：要证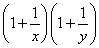≥9成立，         1分

因为x>0,y>0，且x+y=1，所以y=1-x>0.          1分

只需证明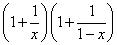≥9，          1分

即证(1+x）(2-x)≥9x(1-x)，           2分

即证2+x-x²≥9x-9x²，即证4x²-4x+1≥0.         1分

即证(2x-1)²≥0，此式显然成立，             2分

所以原不等式成立.                 1分

考点：均值不等式

点评：主要是根据一正二定三相等的思想来求解最值，属于基础题。