题目内容
(12分)已知各项均为正数的数列 ,
,
 的等比中项。
的等比中项。
(1)求证:数列 是等差数列;
是等差数列;
(2)若 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。
【答案】
(1)见解析;(2)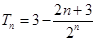
【解析】
试题分析:(1)要证明一个数列是等差数列,关键是证明从第二项起后一项与前一项的差都为同一个常数即可。
(2)在第一问的基础上,进一步结合错位相减法求数列的和。
解。(1)由题意,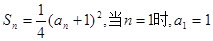
当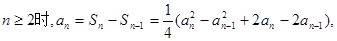
即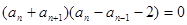
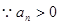
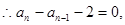
即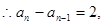
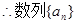 是等差数列
是等差数列
(2)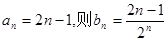
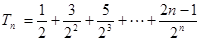 ①
①
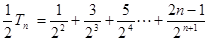 ②
②
①—②得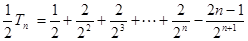
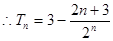
考点:本题主要考查了利用通项公式与前n项和关系式的运用求解得到其通项公式,同时能利用等差数列的定义得到证明,和数列的求和运用。
点评:解决该试题的关键是根据通项公式与前n项和关系式得到其通项公式,以及错位相减法求数列的和的运用。

练习册系列答案
相关题目
 与
与 的大小,并加以证明.
的大小,并加以证明. 与
与 的大小,并加以证明.
的大小,并加以证明. 与
与 的大小,并加以证明.
的大小,并加以证明.