题目内容
已知在四面体ABCD中,E,F分别是AC,BD的中点,若AB=2,CD=4,EF⊥AB,则EF与CD所成的角的度数为分析:设G为AD的中点,连接GF,GE,由三角形中位线定理可得GF∥AB,GE∥CD,则∠GFE即为EF与CD所成的角,结合AB=2,CD=4,EF⊥AB,解△GEF,即可得到答案.
解答: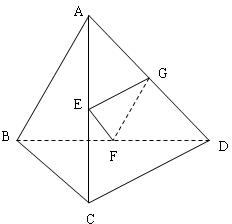 解:设G为AD的中点,连接GF,GE,
解:设G为AD的中点,连接GF,GE,
则GF,GE分别为三角形ABD,三角形ACD的中线.
则GF∥AB,且GF=
AB=1,GE∥CD,且GE=
CD=2,
则EF与CD所成角的度数等于EF与GE所成角的度数
又EF⊥AB,GF∥AB,
∴EF⊥GF
则△GEF为直角三角形,GF=1,GE=2,∠GFE=90°
则在直角△GEF中,sin∠GEF=
∴∠GEF=30°.
故答案为:30°
 解:设G为AD的中点,连接GF,GE,
解:设G为AD的中点,连接GF,GE,则GF,GE分别为三角形ABD,三角形ACD的中线.
则GF∥AB,且GF=
| 1 |
| 2 |
| 1 |
| 2 |
则EF与CD所成角的度数等于EF与GE所成角的度数
又EF⊥AB,GF∥AB,
∴EF⊥GF
则△GEF为直角三角形,GF=1,GE=2,∠GFE=90°
则在直角△GEF中,sin∠GEF=
| 1 |
| 2 |
∴∠GEF=30°.
故答案为:30°
点评:本题考查的知识点是异面直线及其所成的角,其中利用三角形中位线定理,得到GF∥AB,GE∥CD,进而得到∠GFE即为EF与CD所成的角,是解答本题的关键.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
 已知在四面体ABCD中,AC=BD,而且AC⊥BD,E,F,G,H分别是边AB,BC,CD,DA的中点.
已知在四面体ABCD中,AC=BD,而且AC⊥BD,E,F,G,H分别是边AB,BC,CD,DA的中点.