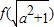题目内容

设函数f（x）在（1，+∞）上是减函数，则f（a），f（2a），f（a2+1），f(
a2+1
)中最小的值是（　　）
A、f（a）
B、f（2a）
C、f（a2+1）
D、f(
a2+1
)
分析：在（1，+∞）上，令a=2，发现a，2a，a2+1，
a2+1
 中a2+1 最大，由于 函数f（x）在（1，+∞）上是减函数，
故f（a2+1）最小．
解答：解：在（1，+∞）上，令a=2，则 2a=4，a2+1=5，
a2+1
=
5
，
∴a2+1 最大，∵函数f（x）在（1，+∞）上是减函数，∴f（a2+1）最小，
故选 C．
点评：本题考查函数的单调性的应用，通过给变量取特殊值，来比较几个式子的大小，是一种简单有效的方法．
练习册系列答案
相关题目
设函数f（x）在（-1，1）上是奇函数，且在（-1，1）上是减函数，若f（1-m）+f（-m）＜0，则m的取值范围是（　　）
已知函数f（x）=-
1
3
x3+（
a
2
-1）x2+ax（a∈R）
（I）证明：函数f（x）总有两个极值点x1，x2且|x1-x2|≥2；
（II）设函数f（x）在（-1，1）上单调递增，求a的取值范围．
设函数f（x）在（1，+∞）上是减函数，则f（a），f（2a），f（a2+1），f(
a2+1
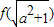)中最小的值是（　　）
A．f（a）B．f（2a）C．f（a2+1）D．f(
a2+1
)
设函数f（x）在（1，+∞）上是减函数，则f（a），f（2a），f（a2+1），中最小的值是（ ）
A．f（a）
B．f（2a）
C．f（a2+1）
D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网