题目内容
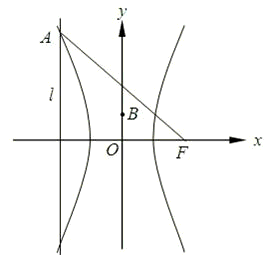 中心在原点的双曲线C1的一个焦点与抛物线C2:y2=8x的焦点F重合,抛物线C2的准线l与双曲线C1的一个交点为A,且|AF|=5.
中心在原点的双曲线C1的一个焦点与抛物线C2:y2=8x的焦点F重合,抛物线C2的准线l与双曲线C1的一个交点为A,且|AF|=5.
(Ⅰ)求双曲线C1的方程;
(Ⅱ)若过点B(0,1)的直线m与双曲线C1相交于不同两点M,N,且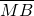 =λ
=λ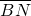 .
.
①求直线m的斜率k的变化范围;
②当直线m的斜率不为0时,问在直线y=x上是否存在一定点C,使 ⊥(
⊥(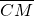 -λ
-λ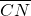 )?若存在,求出点C的坐标;若不存在,请说明理由.
)?若存在,求出点C的坐标;若不存在,请说明理由.
解:(Ⅰ)由条件得F(2,0),l:x=-2.
设所求双曲线方程为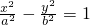 (a>0,b>0),
(a>0,b>0),
直线l与x轴交于F′,根据|AF|=5,|FF′|=4,
得|AF′|=3,
从而 .
.
解得a=1,b= .从而所求的双曲线方程为:x2-
.从而所求的双曲线方程为:x2-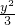 =1;
=1;

(Ⅱ)①设直线m:y=kx+1,代入x2-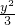 =1得,
=1得,
(3-k2)x2-2kx-4=0,
∵直线m与曲线C1交于两点M,N.
∴ ,
,
解得-2<k<- ,或-
,或- <k<
<k< ,或
,或 <k<2.
<k<2.
②设M,N的坐标分别为(x1,y1),(x2,y2),
由上面可得 ,
,
由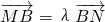 ,得(-x1,1-y1)=λ(x2,y2-1),
,得(-x1,1-y1)=λ(x2,y2-1),
∴x1=-λx2,
设存在点C(t,t),
则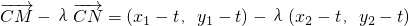
=(x1-λx2+t(λ-1),y1-λy2+t(λ-1)),
又 ,从而由
,从而由 ,
,
得y1-λy2+t(λ-1)=0.
因直线m的斜率不为零,故λ≠1.
所以解得t= =
= =1+k?
=1+k? .
.
因为λ=-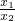 ,代入得t=1+k?
,代入得t=1+k?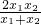 ,
,
因为 ,
,
代入得t=-3,即存在点C(-3,-3),满足要求.
分析:(Ⅰ)设所求双曲线方程为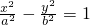 (a>0,b>0),直线l与x轴交于F′,根据|AF|=5,|FF′|=4,能够求出所求的双曲线方程.
(a>0,b>0),直线l与x轴交于F′,根据|AF|=5,|FF′|=4,能够求出所求的双曲线方程.
(Ⅱ)设直线m:y=kx+1,代入x2-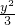 =1得,(3-k2)x2-2kx-4=0,由直线m与曲线C1交于两点M,N,能求出-2<k<-
=1得,(3-k2)x2-2kx-4=0,由直线m与曲线C1交于两点M,N,能求出-2<k<- ,或-
,或- <k<
<k< ,或
,或 <k<2.设M,N的坐标分别为(x1,y1),(x2,y2),得
<k<2.设M,N的坐标分别为(x1,y1),(x2,y2),得 ,由
,由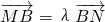 ,得(-x1,1-y1)=λ(x2,y2-1),所以x1=-λx2,由此入手能够求出存在点C(-3,-3),满足要求.
,得(-x1,1-y1)=λ(x2,y2-1),所以x1=-λx2,由此入手能够求出存在点C(-3,-3),满足要求.
点评:通过几何量的转化考查用待定系数法求曲线方程的能力,通过直线与圆锥曲线的位置关系处理,考查学生的运算能力.通过向量与几何问题的综合,考查学生分析转化问题的能力,探究研究问题的能力,并体现了合理消元,设而不解的代数变形的思想.本题综合性强,是高考的重点,易错点是知识体系不牢固.
设所求双曲线方程为
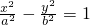 (a>0,b>0),
(a>0,b>0),直线l与x轴交于F′,根据|AF|=5,|FF′|=4,
得|AF′|=3,
从而
 .
.解得a=1,b=
 .从而所求的双曲线方程为:x2-
.从而所求的双曲线方程为:x2-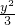 =1;
=1;
(Ⅱ)①设直线m:y=kx+1,代入x2-
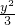 =1得,
=1得,(3-k2)x2-2kx-4=0,
∵直线m与曲线C1交于两点M,N.
∴
 ,
,解得-2<k<-
 ,或-
,或- <k<
<k< ,或
,或 <k<2.
<k<2.②设M,N的坐标分别为(x1,y1),(x2,y2),
由上面可得
 ,
,由
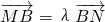 ,得(-x1,1-y1)=λ(x2,y2-1),
,得(-x1,1-y1)=λ(x2,y2-1),∴x1=-λx2,
设存在点C(t,t),
则
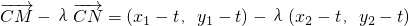
=(x1-λx2+t(λ-1),y1-λy2+t(λ-1)),
又
 ,从而由
,从而由 ,
,得y1-λy2+t(λ-1)=0.
因直线m的斜率不为零,故λ≠1.
所以解得t=
 =
= =1+k?
=1+k? .
.因为λ=-
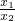 ,代入得t=1+k?
,代入得t=1+k?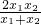 ,
,因为
 ,
,代入得t=-3,即存在点C(-3,-3),满足要求.
分析:(Ⅰ)设所求双曲线方程为
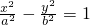 (a>0,b>0),直线l与x轴交于F′,根据|AF|=5,|FF′|=4,能够求出所求的双曲线方程.
(a>0,b>0),直线l与x轴交于F′,根据|AF|=5,|FF′|=4,能够求出所求的双曲线方程.(Ⅱ)设直线m:y=kx+1,代入x2-
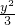 =1得,(3-k2)x2-2kx-4=0,由直线m与曲线C1交于两点M,N,能求出-2<k<-
=1得,(3-k2)x2-2kx-4=0,由直线m与曲线C1交于两点M,N,能求出-2<k<- ,或-
,或- <k<
<k< ,或
,或 <k<2.设M,N的坐标分别为(x1,y1),(x2,y2),得
<k<2.设M,N的坐标分别为(x1,y1),(x2,y2),得 ,由
,由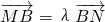 ,得(-x1,1-y1)=λ(x2,y2-1),所以x1=-λx2,由此入手能够求出存在点C(-3,-3),满足要求.
,得(-x1,1-y1)=λ(x2,y2-1),所以x1=-λx2,由此入手能够求出存在点C(-3,-3),满足要求.点评:通过几何量的转化考查用待定系数法求曲线方程的能力,通过直线与圆锥曲线的位置关系处理,考查学生的运算能力.通过向量与几何问题的综合,考查学生分析转化问题的能力,探究研究问题的能力,并体现了合理消元,设而不解的代数变形的思想.本题综合性强,是高考的重点,易错点是知识体系不牢固.

练习册系列答案
相关题目