题目内容
(13分)已知![]() ,
,![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,
, ![]() .
.
(Ⅰ)求证:数列![]() 是等比数列;
是等比数列;
(Ⅱ)当n取何值时,![]() 取最大值,并求出最大值;
取最大值,并求出最大值;
(III)若![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
解析:(I)∵![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
即![]() .
.
又![]() ,可知对任何
,可知对任何![]() ,
,![]() ,
,
所以![]() .……………………………2分
.……………………………2分
∵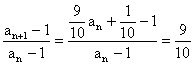 ,
,
∴![]() 是以
是以![]() 为首项,公比为
为首项,公比为![]() 的等比数列.………4分
的等比数列.………4分
(II)由(I)可知![]() =
=![]() (
(![]() ).
).
∴![]() .
.
 .……………………………5分
.……………………………5分
当n=7时,![]() ,
,![]() ;
;
当n<7时,![]() ,
,![]() ;
;
当n>7时,![]() ,
,![]() .
.
∴当n=7或n=8时,![]() 取最大值,最大值为
取最大值,最大值为![]() .……8分
.……8分
(III)由![]() ,得
,得![]() (*)
(*)
依题意(*)式对任意![]() 恒成立,
恒成立,
①当t=0时,(*)式显然不成立,因此t=0不合题意.…………9分
②当t<0时,由![]() ,可知
,可知![]() (
(![]() ).
).
而当m是偶数时![]() ,因此t<0不合题意.…………10分
,因此t<0不合题意.…………10分
③当t>0时,由![]() (
(![]() ),
),
∴![]() ∴
∴![]() . (
. (![]() )……11分
)……11分
设![]() (
(![]() )
)
∵![]() =
=![]() ,
,
∴![]() .
.
∴![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
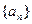 ,定义其倒均数是
,定义其倒均数是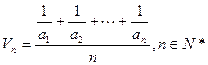 。
。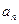 }的倒均数是
}的倒均数是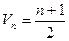 ,求数列{
,求数列{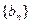 的首项为-1,公比为
的首项为-1,公比为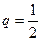 ,其倒数均为
,其倒数均为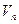 ,若存在正整数k,使
,若存在正整数k,使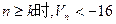 恒成立,试求k的最小值。
恒成立,试求k的最小值。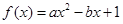 ,分别从集合P和Q中随机取一个数a和b得到数列
,分别从集合P和Q中随机取一个数a和b得到数列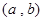 。
。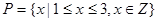 ,
,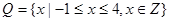 ,列举出所有的数对
,列举出所有的数对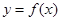 有零点的概率;
有零点的概率;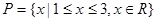 ,
,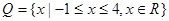 ,求函数
,求函数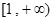 上是增函数的概率。
上是增函数的概率。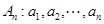 .如果数列
.如果数列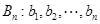 满足
满足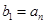 ,
,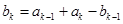 ,其中
,其中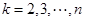 ,则称
,则称 为
为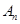 的“衍生数列”.
的“衍生数列”.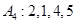 的“衍生数列”
的“衍生数列”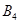 ;
; 为偶数,且
为偶数,且 ;
; 为奇数,且
为奇数,且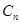 ,….依次将数
,….依次将数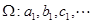 .证明:
.证明: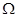 是等差数列.
是等差数列.