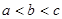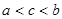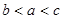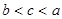题目内容
(选修4-5)已知函数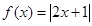 ,
, 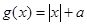
(Ⅰ)当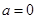 时,解不等式
时,解不等式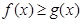 ;
;
(Ⅱ)若存在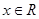 ,使得
,使得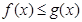 成立,求实数
成立,求实数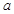 的取值范围.
的取值范围.
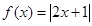 ,
, 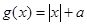
(Ⅰ)当
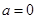 时,解不等式
时,解不等式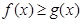 ;
;(Ⅱ)若存在
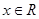 ,使得
,使得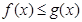 成立,求实数
成立,求实数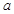 的取值范围.
的取值范围.(Ⅰ)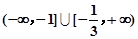 ;(Ⅱ)
;(Ⅱ)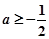 。
。
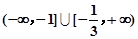 ;(Ⅱ)
;(Ⅱ)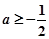 。
。(1))当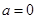 时,
时,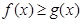 等价于
等价于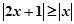 ,两边平方整理
,两边平方整理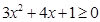 ,
,
转化为解一元二次不等式;(2)由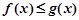 得
得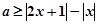 ,只需
,只需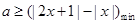 ,去掉绝对值符号分段求解得最小值.
,去掉绝对值符号分段求解得最小值.
解:(Ⅰ)当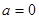 时,由
时,由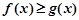 得
得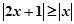 ,两边平方整理得
,两边平方整理得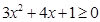 ……2分
……2分
解之得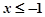 或
或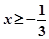 ∴原不等式的解集为
∴原不等式的解集为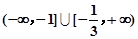 ……5分
……5分
(Ⅱ)由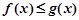 得
得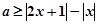 ……6分,
……6分,
令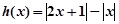 ,则
,则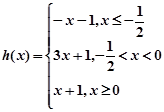 ……8分
……8分
故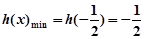 ,从而所求实数
,从而所求实数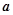 的范围为
的范围为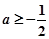 ……10分
……10分
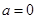 时,
时,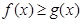 等价于
等价于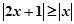 ,两边平方整理
,两边平方整理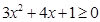 ,
,转化为解一元二次不等式;(2)由
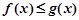 得
得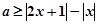 ,只需
,只需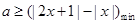 ,去掉绝对值符号分段求解得最小值.
,去掉绝对值符号分段求解得最小值.解:(Ⅰ)当
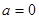 时,由
时,由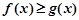 得
得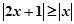 ,两边平方整理得
,两边平方整理得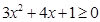 ……2分
……2分解之得
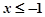 或
或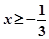 ∴原不等式的解集为
∴原不等式的解集为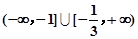 ……5分
……5分(Ⅱ)由
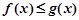 得
得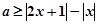 ……6分,
……6分,令
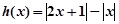 ,则
,则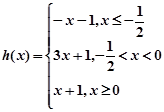 ……8分
……8分 故
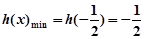 ,从而所求实数
,从而所求实数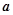 的范围为
的范围为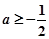 ……10分
……10分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
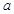 <
<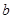 <0,①
<0,①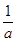 >
>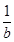 ;②
;②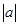 >
>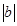 ;③
;③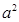 >
>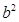 ;④
;④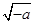 <
<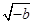 ,上述不等式中正确的个数为( )
,上述不等式中正确的个数为( )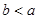 ,
,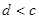 ,则下列不等式中一定成立的是 ( )
,则下列不等式中一定成立的是 ( )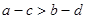
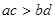
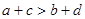
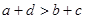
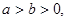 则不等式:①
则不等式:①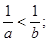 ②
②
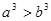 ;③
;③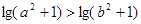 ;
;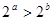 ,其中成立的是 ( )
,其中成立的是 ( )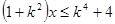 的解集是M,则对任意常数k,总有( ).
的解集是M,则对任意常数k,总有( ).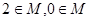
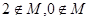
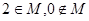
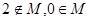
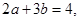 则
则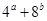 的最小值为( )
的最小值为( )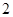
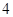
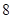
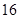
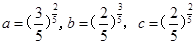 ,则a,b,c的大小关系是
,则a,b,c的大小关系是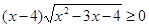 的解集是____________.
的解集是____________.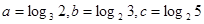 ,下面不等式成立的是( )
,下面不等式成立的是( )