题目内容
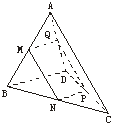
如图是一个四面体形状的木块ABCD,用平行于一组对棱AC、BD的平面截此四面体得截面PQMN,解答下列各问题: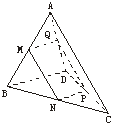
(1)四边形PQMN是平行四边形吗?试证明.
(2)若AC=BD,能截得菱形吗?
(3)在什么情况下,可以截得一个矩形?
(4)在什么情况下,可以截得一个正方形?
(5)若AC=BD=a,求证平行四边形PQMN的周长是定值.
答案:
解析:
解析:
| 解:(1)∵AC∥面PQMN,面PQMN∩面ACD=PQ,
且AC 同理可证AC∥MN,BD∥MQ,BD∥NP,∴PQ∥MN,MQ∥NP. ∴四边形PQMN是平行四边形. (2)若AC=BD,由三角形中位线定理可知,当点P是AD中点时,四边形PQMN是菱形. (3)显然,当AC⊥BD时,四边形PQMN是矩形. (4)由(2)、(3)可知当AC⊥BD且AC=BD时,四边形PQMN是正方形. (5)设MQ=x,PQ=y,AQ∶QD=m∶n. ∵△AMQ∽△ABD,∴MQ∶BD=AQ∶AD=m∶(m+n), ∴MQ=am∶(m+n),即x=am∶(m+n). 同理可得y=an∶(m+n). ∴x+y=a. ∴周长=2(x+y)=2a, 即当AC=BD=a时,平行四边形PQMN的周长是定值2a.
|

练习册系列答案
相关题目