题目内容
已知直线 :
: (k
(k R)与圆C:
R)与圆C: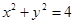 相交于点A、B, M为弦AB中点.
相交于点A、B, M为弦AB中点.
(Ⅰ) 当k=1时,求弦AB的中点M的坐标及AB弦长;
(Ⅱ)求证:直线 与圆C总有两个交点;
与圆C总有两个交点;
(Ⅲ)当k变化时求弦AB的中点M的轨迹方程.
【答案】
(1) ;(2)见解析;(3)
;(2)见解析;(3)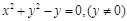 .
.
【解析】(1)先直线方程与圆的方程联立,求交点坐标,再求弦长问题、中点坐标;(2)直线过定点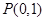 ,其在圆内;3()利用直线斜率乘积为-1,求轨迹方程.
,其在圆内;3()利用直线斜率乘积为-1,求轨迹方程.
解 :(Ⅰ)当k=1时,由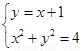 得
得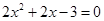
设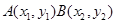 ,,则
,,则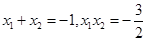
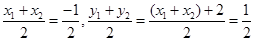 .∴
.∴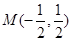 .
. 
(Ⅱ)直线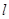 :
: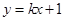 (
(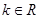 )过定点
)过定点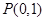 且P在圆内∴直线与圆总有两个交点
且P在圆内∴直线与圆总有两个交点
(Ⅲ)∵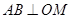 ,直线
,直线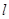 :
: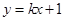 (
(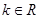 )过定点
)过定点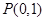
∴点M在以OP为直经的圆周上.∴设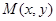
∵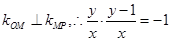
∴点M的轨迹方程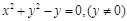 .
.

练习册系列答案
相关题目