题目内容
在△ABC中,a,b,c分别为角A,B,C的对边,三边a,b,c成等差数列,且B=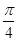 ,则|cos A-cos C|的值为________.
,则|cos A-cos C|的值为________.
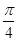 ,则|cos A-cos C|的值为________.
,则|cos A-cos C|的值为________.
由已知得2b=a+c,根据正弦定理得2sin B=sin A+sin C,代入B=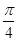 得sin A+sin C=
得sin A+sin C= ,两端平方得sin2A+2sin Asin C+sin2C=2.①
,两端平方得sin2A+2sin Asin C+sin2C=2.①
设|cos A-cos C|=t,两端平方得cos2A-2cos Acos C+cos2C=t2,②
①+②得2-2cos(A+C)=2+t2,即2cos B=t2,即t2= ,t≥0,得t=
,t≥0,得t= .
.
所以|cos A-cos C|= .
.
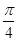 得sin A+sin C=
得sin A+sin C= ,两端平方得sin2A+2sin Asin C+sin2C=2.①
,两端平方得sin2A+2sin Asin C+sin2C=2.①设|cos A-cos C|=t,两端平方得cos2A-2cos Acos C+cos2C=t2,②
①+②得2-2cos(A+C)=2+t2,即2cos B=t2,即t2=
 ,t≥0,得t=
,t≥0,得t= .
.所以|cos A-cos C|=
 .
.
练习册系列答案
相关题目
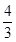 ,sin(α+β)=
,sin(α+β)=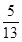 ,其中α,β∈(0,π),则sin α的值为________.
,其中α,β∈(0,π),则sin α的值为________.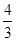 ,sin(α+β)=
,sin(α+β)=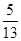 ,其中α,β∈(0,π),则sin α的值为( ).
,其中α,β∈(0,π),则sin α的值为( ).


 ,则
,则 ( )
( )



 ,则
,则 的值为
的值为



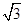 )·sin40°.
)·sin40°.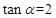 ,那么
,那么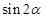 的值是( )
的值是( )



 =( )
=( )  ,则
,则 ( )
( )


