题目内容
已知直线l1:ax+2y+6=0和直线l2:x+(a-1)y+a2-1=0,
(1)试判断l1与l2是否平行;
(2)l1⊥l2时,求a的值.
(1)试判断l1与l2是否平行;
(2)l1⊥l2时,求a的值.
(1)a=-1时,l1∥l2(2)a=

(1)方法一 当a=1时,l1:x+2y+6=0,
l2:x=0,l1不平行于l2;
当a=0时,l1:y=-3,
l2:x-y-1=0,l1不平行于l2;
当a≠1且a≠0时,两直线可化为
l1:y=- -3,l2:y=
-3,l2:y= -(a+1),
-(a+1),
l1∥l2
 ,解得a="-1, "
,解得a="-1, "
综上可知,a=-1时,l1∥l2,否则l1与l2不平行.
方法二 由A1B2-A2B1=0,得a(a-1)-1×2=0,
由A1C2-A2C1≠0,得a(a2-1)-1×6≠0,
∴l1∥l2



 a="-1, "
a="-1, "
故当a=-1时,l1∥l2,否则l1与l2不平行.
(2)方法一 当a=1时,l1:x+2y+6=0,l2:x=0,
l1与l2不垂直,故a=1不成立. 当a≠1时,l1:y=- x-3,
x-3,
l2:y= -(a+1), 由
-(a+1), 由 ·
· =-1
=-1 a=
a= .
.
方法二 由A1A2+B1B2=0,得a+2(a-1)=0 a=
a= .
.
l2:x=0,l1不平行于l2;
当a=0时,l1:y=-3,
l2:x-y-1=0,l1不平行于l2;
当a≠1且a≠0时,两直线可化为
l1:y=-
 -3,l2:y=
-3,l2:y= -(a+1),
-(a+1),l1∥l2

 ,解得a="-1, "
,解得a="-1, " 综上可知,a=-1时,l1∥l2,否则l1与l2不平行.
方法二 由A1B2-A2B1=0,得a(a-1)-1×2=0,
由A1C2-A2C1≠0,得a(a2-1)-1×6≠0,
∴l1∥l2




 a="-1, "
a="-1, " 故当a=-1时,l1∥l2,否则l1与l2不平行.
(2)方法一 当a=1时,l1:x+2y+6=0,l2:x=0,
l1与l2不垂直,故a=1不成立. 当a≠1时,l1:y=-
 x-3,
x-3,l2:y=
 -(a+1), 由
-(a+1), 由 ·
· =-1
=-1 a=
a= .
. 方法二 由A1A2+B1B2=0,得a+2(a-1)=0
 a=
a= .
. 
练习册系列答案
相关题目
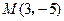 ,过
,过 的直线与
的直线与 轴和
轴和 轴分别交于
轴分别交于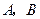 两点,若
两点,若 的中点,求
的中点,求

 ,-2
,-2
 点射出,到
点射出,到 轴上的
轴上的 点后被
点后被 轴上的
轴上的 点,又被
点,又被 ,求
,求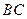 所在直线的方程.
所在直线的方程.