题目内容
(04年天津卷理)(12分)
已知定义在R上的函数![]() 和数列
和数列![]() 满足下列条件:
满足下列条件:
![]() ,
,
![]()
其中![]() 为常数,
为常数,![]() 为非零常数。
为非零常数。
(I)令![]() ,证明数列
,证明数列![]() 是等比数列;
是等比数列;
(II)求数列![]() 的通项公式;
的通项公式;
(III)当![]() 时,求
时,求![]()
解析:(I)证明:由![]() 可得
可得
![]()
由数学归纳法可证 ![]()
![]()
由题设条件,当![]() 时
时
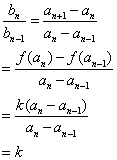
因此,数列![]() 是一个公比为
是一个公比为![]() 的等比数列。。。。。。。。。。。。。。。。。4分
的等比数列。。。。。。。。。。。。。。。。。4分
(II)解:由(I)知,![]()
![]()
当 ![]() 时
时
![]()
![]()
当 ![]() 时
时
![]()
![]()
而 ![]()
![]()
所以,当![]() 时
时
![]()
上式对![]() 也成立。所以,数列
也成立。所以,数列![]() 的通项公式为
的通项公式为
![]()
当![]() 时
时
![]()
上式对![]() 也成立。所以,数列
也成立。所以,数列![]() 的通项公式为
的通项公式为
![]() 。
。
(III)解:当![]() 时
时
![]()
![]() 。。。。。。。。。。。。。。。。。。12分
。。。。。。。。。。。。。。。。。。12分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目