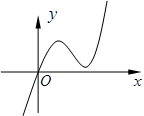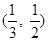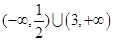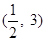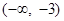题目内容
函数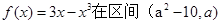 上有最小值,实数a的取值范围是( )
上有最小值,实数a的取值范围是( )
| A.(-1,3) | B.(-1,2) | C.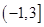  | D.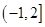 |
D
解析试题分析:由题 f'(x)=3-3x2,令f'(x)>0解得-1<x<1;令f'(x)<0解得x<-1或x>1,由此得函数在(-∞,-1)上是减函数,在(-1,1)上是增函数,在(1,+∞)上是减函数
故函数在x=-1处取到极小值-2,判断知此极小值必是区间(a2-12,a)上的最小值.∴a2-12<-1<a,解得-1<a<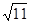 ,又当x=2时,f(2)=-2,故有a≤2,综上知a∈(-1,2],故选D.
,又当x=2时,f(2)=-2,故有a≤2,综上知a∈(-1,2],故选D.
考点:用导数研究函数的最值

练习册系列答案
相关题目
已知 为常数,则使得
为常数,则使得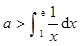 成立的一个充分而不必要条件是 ( )
成立的一个充分而不必要条件是 ( )
A. | B.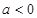 | C.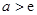 | D. |
若函数 的图象上任意点处切线的倾斜角为
的图象上任意点处切线的倾斜角为 ,则
,则 的最小值是( )
的最小值是( )
A.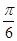 | B. | C. | D.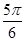 |
若方程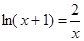 的根在区间
的根在区间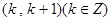 上,则
上,则 的值为( )
的值为( )
A.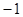 | B.1 | C.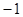 或2 或2 | D.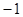 或1 或1 |
函数 的单调递增区间是( )
的单调递增区间是( )
A.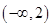 | B.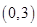 | C.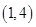 | D.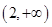 |
设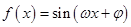 ,其中
,其中 ,则
,则 是偶函数的充要条件是( )
是偶函数的充要条件是( )
A.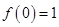 | B.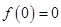 | C.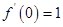 | D.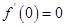 |
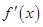 是函数
是函数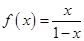 的导数,则
的导数,则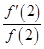 的值是( )
的值是( )
A.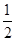 | B. | C.2 | D.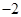 |
定义:符合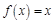 的
的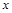 称为
称为 的一阶不动点,符合
的一阶不动点,符合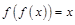 的
的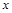 称为
称为 的二阶不动点。设函数
的二阶不动点。设函数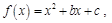 若函数
若函数 没有一阶不动点,则函数
没有一阶不动点,则函数 二阶不动点的个数为 ( )
二阶不动点的个数为 ( )
| A.四个 | B.两个 | C.一个 | D.零个 |
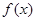 满足
满足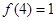 .
.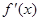 为
为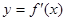 的图象如图所示.若两正数
的图象如图所示.若两正数 满足
满足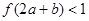 ,则
,则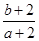 的取值范围是( )
的取值范围是( )