题目内容
一个几何体的三视图如图所示,其中主视图和左视图是腰长为1的两个全等的等腰直角三角形,则该几何体的外接球的表面积为( )
A. | B. | C. | D. |
C
解析试题分析:把原来的几何体补成以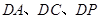 为长、宽、高的长方体,原几何体四棱锥与长方体是同一个外接球,
为长、宽、高的长方体,原几何体四棱锥与长方体是同一个外接球,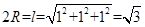 ,
,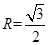 ,
,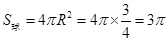 .
.
考点:1.补体法;2.几何体与外接球之间的元素换算.

练习册系列答案
相关题目
直三棱柱ABC-A1B1C1的直观图及三视图如下图所示,D为AC的中点,则下列命题是假命题的是( )
| A.AB1∥平面BDC1 |
| B.A1C⊥平面BDC1 |
| C.直三棱柱的体积V=4 |
D.直三棱柱的外接球的表面积为4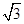 π π |
一个几何体的三视图如图所示,正视图和侧视图都是等边三角形,且该几何体的四个点在空间直角坐标系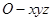 中构坐标分别是(0,0,0),(2,0,0),(2,2,0),(0,2,0),则第五个顶点的坐标可能为( )
中构坐标分别是(0,0,0),(2,0,0),(2,2,0),(0,2,0),则第五个顶点的坐标可能为( )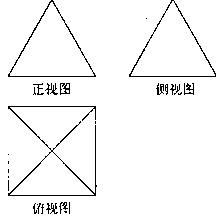
| A.(1,1,1) |
B.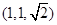 |
C.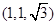 |
D.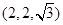 |
设三棱柱的侧棱垂直于底面,所有棱的长都为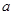 ,顶点都在一个球面上,则该球的表面积为( )
,顶点都在一个球面上,则该球的表面积为( )
A.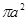 | B.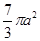 | C.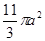 | D.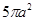 |
一简单组合体的三视图及尺寸如下图所示(单位:  )则该组合体的体积为 ( )
)则该组合体的体积为 ( )
A.72000 | B.64000 | C.56000 | D.44000 |
某几何函数的三视图如图所示,则该几何的体积为( )
| A.18+8π | B.8+8π |
| C.16+16π | D.8+16π |


 中,
中, 、
、 分别是
分别是 、
、 的中点,且
的中点,且 ,若侧棱
,若侧棱 ,则正三棱锥
,则正三棱锥