题目内容
设 是
是 的两个非空子集,如果存在一个从
的两个非空子集,如果存在一个从 到
到 的函数
的函数 满足:(i)
满足:(i) ;(ii)对任意
;(ii)对任意 ,当
,当 时,恒有
时,恒有 .那么称这两个集合“保序同构”.现给出以下4对集合.①
.那么称这两个集合“保序同构”.现给出以下4对集合.① ;②
;② ;③
;③ ;④
;④ ,其中,“保序同构”的集合对的对应的序号是 (写出所有“保序同构”的集合对的对应的序号).
,其中,“保序同构”的集合对的对应的序号是 (写出所有“保序同构”的集合对的对应的序号).
②③④.
解析试题分析:“保序同构”的集合是指存在一函数 满足:(1).S是
满足:(1).S是 的定义域,T是值域,(2).
的定义域,T是值域,(2).  在S上递增.对于①,若任意
在S上递增.对于①,若任意 ,当
,当 时,可能有
时,可能有 ,不是恒有
,不是恒有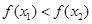 成立,所以①中的两个集合不一定是保序同构,对于②,取
成立,所以①中的两个集合不一定是保序同构,对于②,取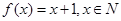 符合保序同构定义,对于③,取函数
符合保序同构定义,对于③,取函数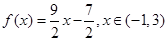 符合保序同构定义,对于④,取
符合保序同构定义,对于④,取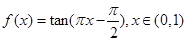 符合保序同构定义,故选②③④.
符合保序同构定义,故选②③④.
考点:新概念信息题,单调函数的概念,蕴含映射思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设全集为 ,集合
,集合 ,则
,则 ( ).
( ).
A. | B.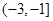 | C. | D. |
已知集合 ,
, ,则
,则 ( ).
( ).
A. | B. | C. | D. |
设集合U=R,集合M= ,P=
,P= ,则下列关系正确的是( )
,则下列关系正确的是( )
| A.M=P | B.(CUM) P= P= | C.P M M | D.M P P |
已知集合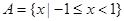 ,
,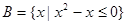 ,则
,则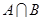 等于( )
等于( )
A.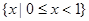 | B.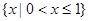 |
C.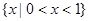 | D.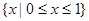 |
已知集合 ,集合
,集合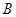 为整数集,则
为整数集,则 ( )
( )
A. | B. | C. | D. |
已知集合A={ },B={
},B={ },则
},则 =( )
=( )
| A.{1,2,3} | B.{0,1,2,3} |
| C.{0,1,2,3,4} | D.{1,2,3,4} |
 则
则 等于 ( )
等于 ( )