题目内容
17.如图,若函数y=f(x)的图象在点P处的切线方程为x-y+2=0,则f(1)+f′(1)=4.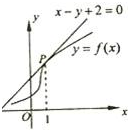
分析 观察图象可得点P(1,f(1))在切线x-y+2=0上,故可求出f(1);由导数的几何意义可得图象在点P处的切线的斜率k=f′(1),由此求出f′(1),即可得到结论.
解答 解:∵点P(1,f(1))在切线x-y+2=0上,
∴1-f(1)+2=0,
解得f(1)=3;
又∵f′(1)=k=1,
∴f(1)+f′(1)=4,
故答案为:4
点评 本题主要考查导数的几何意义的应用,解决切线问题时,要充分利用导数的几何意义结合数形结合的知识来解决.

练习册系列答案
相关题目
6.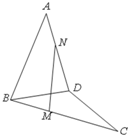 如图,空间四边形ABCD中,M、N分别是BC、DA上的点,且BM:MC=AN:ND=1:2,又AB=5,CD=3,MN与AB、CD所成的角分别为α,β,则之间的大小关系为( )
如图,空间四边形ABCD中,M、N分别是BC、DA上的点,且BM:MC=AN:ND=1:2,又AB=5,CD=3,MN与AB、CD所成的角分别为α,β,则之间的大小关系为( )
 如图,空间四边形ABCD中,M、N分别是BC、DA上的点,且BM:MC=AN:ND=1:2,又AB=5,CD=3,MN与AB、CD所成的角分别为α,β,则之间的大小关系为( )
如图,空间四边形ABCD中,M、N分别是BC、DA上的点,且BM:MC=AN:ND=1:2,又AB=5,CD=3,MN与AB、CD所成的角分别为α,β,则之间的大小关系为( )| A. | α<β | B. | α>β | C. | α=β | D. | 不确定 |
7.等差数列{an}的首项a1=-5,它的前11项平均值为5,若从中抽去一项,余下的平均值为4.6,则抽去的是( )
| A. | a6 | B. | a8 | C. | a9 | D. | a10 |
 如图,点P是正方形ABCD外一点,PA⊥平面ABCD,PA=AB=2,且E,F分别是AB,PC的中点.
如图,点P是正方形ABCD外一点,PA⊥平面ABCD,PA=AB=2,且E,F分别是AB,PC的中点.